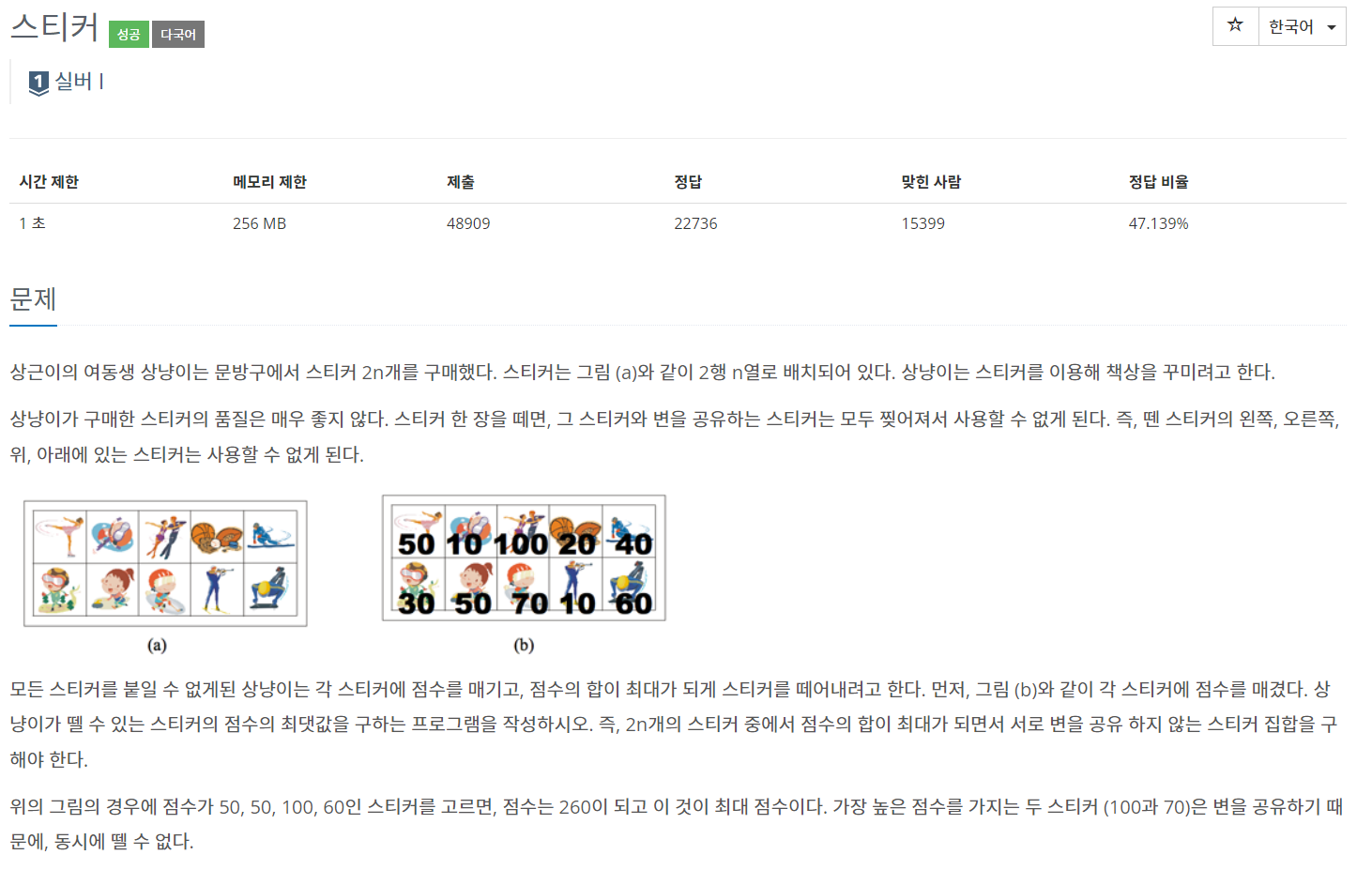
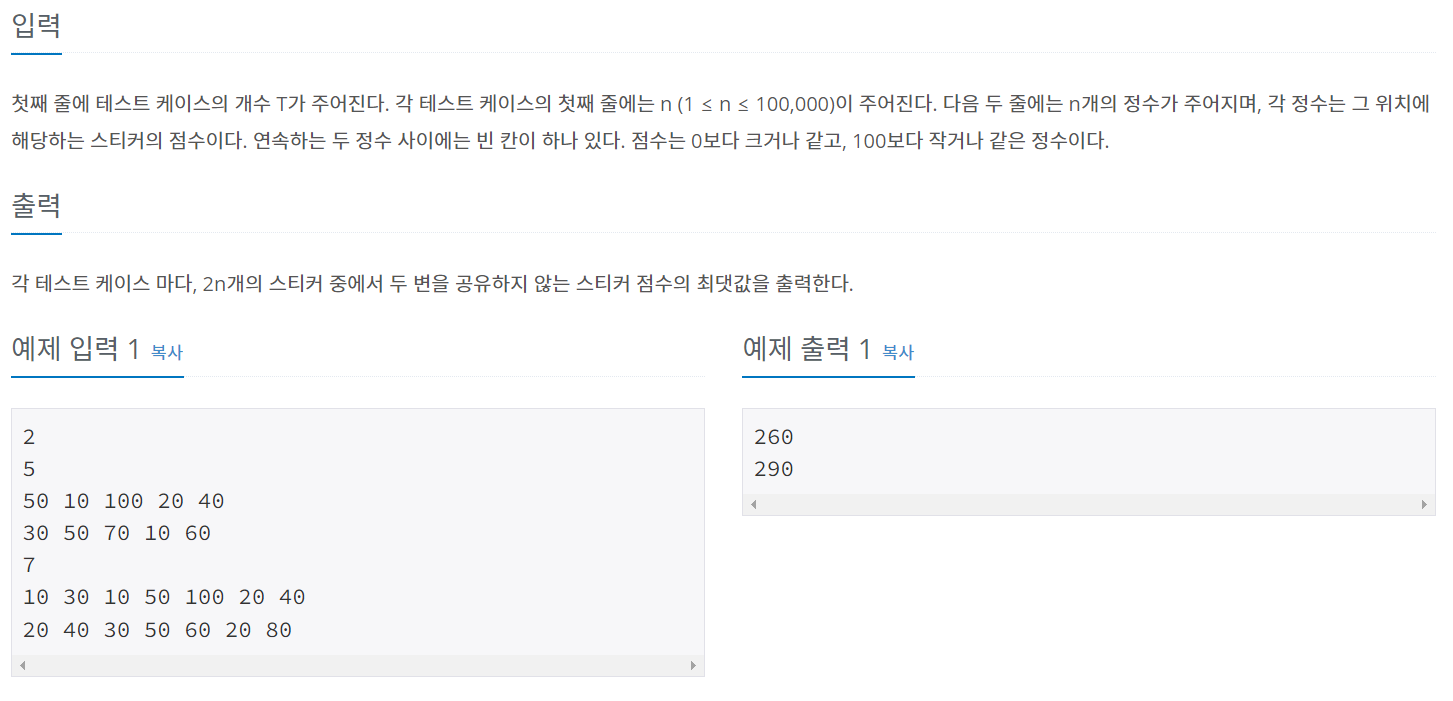
이 문제는 2줄에 총 2 x N개의 자료가 들어왔을 때 주어진 조건에 따라 가장 큰 합을 구하는 문제입니다.
이 문제를 예제의 첫 번째 경우를 예로 들어 설명하겠습니다.
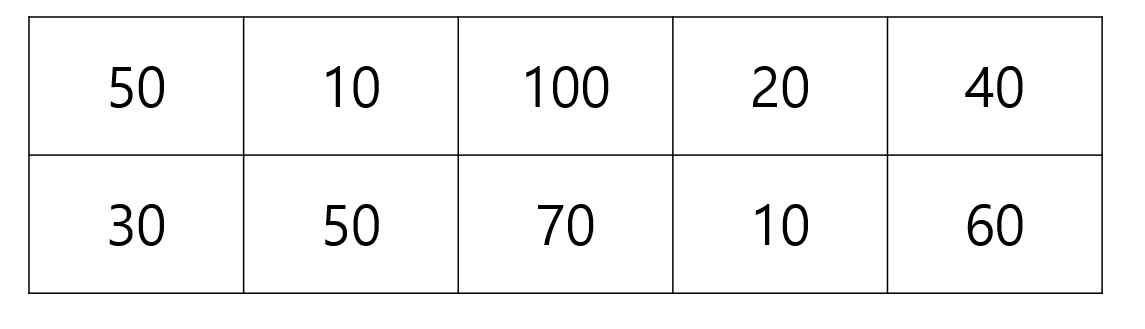
예시를 표로 나타내면 이렇게 됩니다.
이 표에서는 1번째 column에서 무조건 1개의 항을 선택해야 합니다.
그 이유는 2번째 column에서 혹은 3번째 column에서 어떠한 항을 선택하더라도 첫 번째 column에서 선택할 수 있는 항이 남기 때문입니다. 이를 그림으로 설명해드리겠습니다.
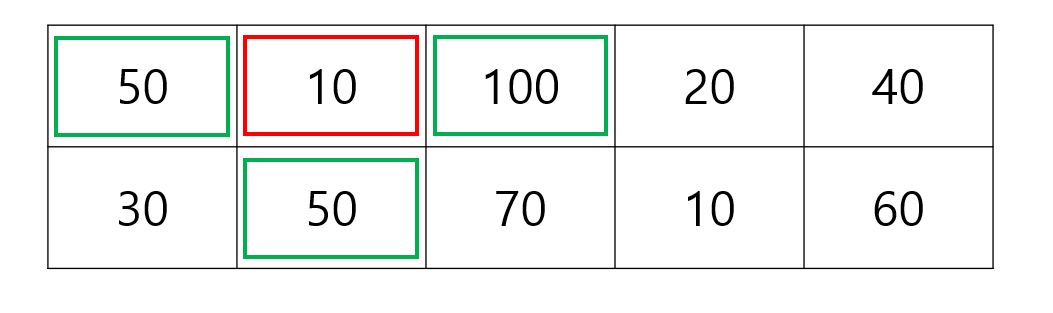
저는 선택한 항을 빨간 박스로 표시했고 그 주변에 문제에 따라서 찢어져서 사용할 수 없는 스티커들을 초록백 박스로
표시하였습니다.
이 경우에 1번 column에서 30이 추가가 될 수 있습니다.
반대로 2번 column에서 10이 아닌 50을 선택하여도 1번 column에서 선택할 수 있는 칸이 50으로 바뀔 뿐 같습니다.
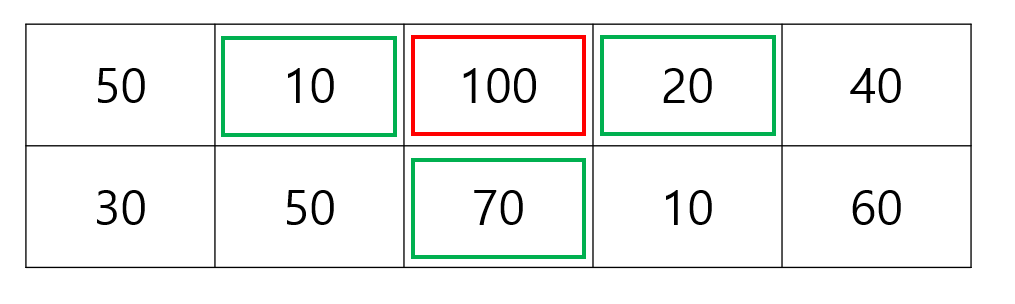
3번 column에서 첫 번째 항을 선택하여도 1번 column에 선택할 수 있는 항들이 있기 때문에 우리는 선택할 스티커에
첫 번째 column에 있는 스티커가 무조건 들어간다는 것을 알 수 있습니다.
이제 우리는 스티커가 어떤 방식으로 선택할 수 있는지를 알아봐야 합니다.
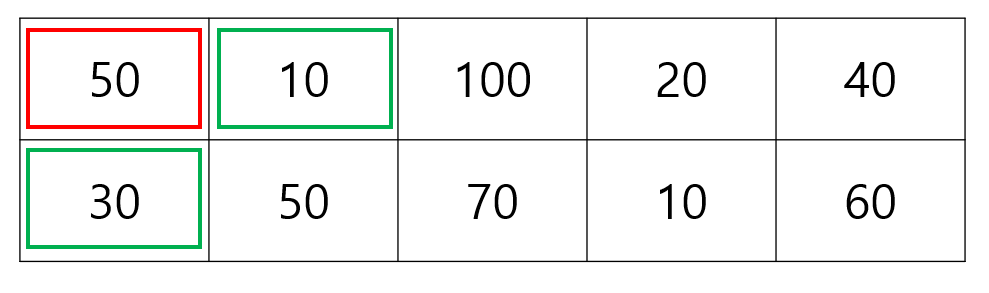
첫 번째 스티커로 1번 column에 있는 50이 선택되었다고 가정해보겠습니다.
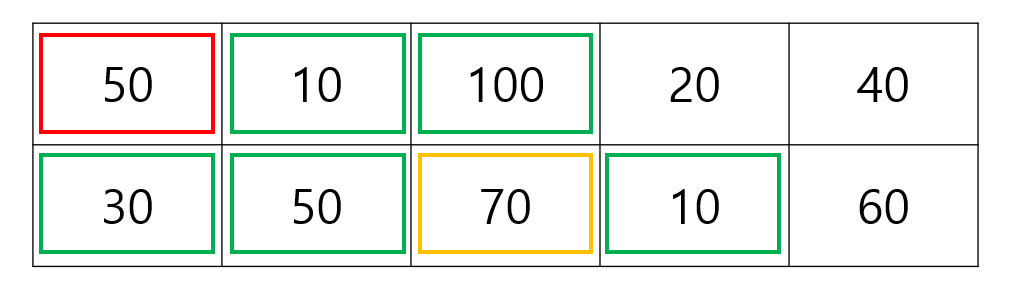
선택한 스티커는 빨간 박스로 문제의 조건에 의해서 찢어진 스티커를 초록 박스로 표시하겠습니다.
이때 우리는 1 2 3 4 5번 column 순으로 연산을 진행해 나갈 것인데 이미 지나간 column에서는 선택할 수 있는 스티커를
남기지 않을 것입니다.
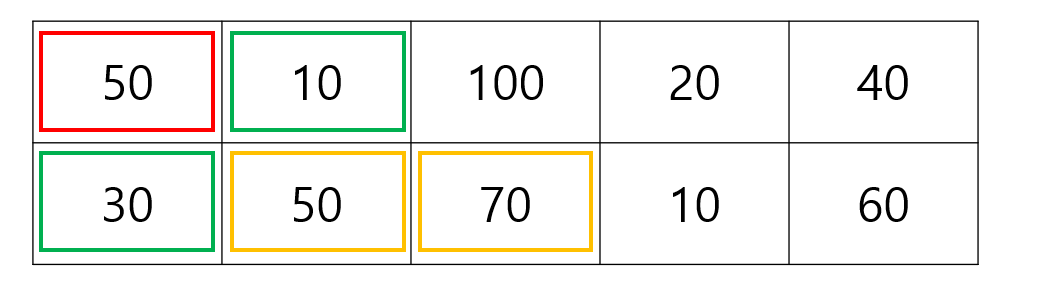
그렇다면 우리가 선택할 수 있는 스티커는 주황색 박스로 감싸진 2개의 스티커가 있습니다.
이 두 개의 스티커를 선택하면 각각 어떻게 되는지 보여드리겠습니다.
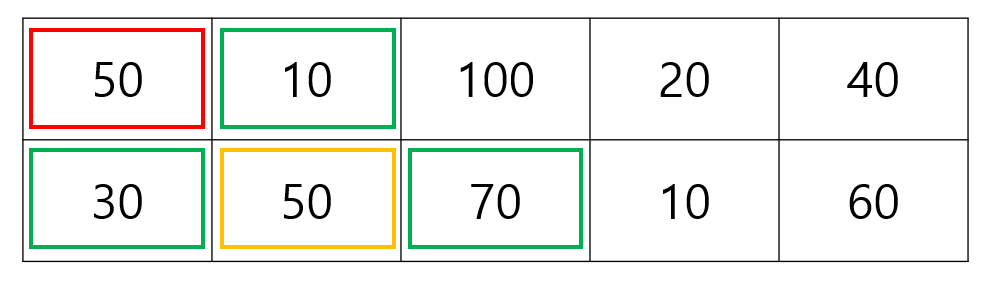
어떤 스티커를 선택하던지 이미 지나간 column에는 선택할 수 있는 스티커가 없다는 것을 알 수 있습니다.
스티커를 이렇게 선택할 수 있다는 것을 염두에 두고 코드를 짜도록 하겠습니다.
import java.util.*;
import java.io.*;
public class Main{
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringBuffer sb = new StringBuffer();
int T = Integer.parseInt(br.readLine());
while(T-->0){
int N = Integer.parseInt(br.readLine());
int[][] sticker = new int[2][N+1];
int[][] dp = new int[2][N+1];
for(int i = 0; i<2; i++){
StringTokenizer st = new StringTokenizer(br.readLine());
for(int j = 1; j<=N; j++)
sticker[i][j] = Integer.parseInt(st.nextToken());
}
dp[0][1] = sticker[0][1];
dp[1][1] = sticker[1][1];
for(int i = 2; i<=N; i++){
dp[0][i] = Math.max(dp[1][i-1], dp[1][i-2]) + sticker[0][i];
dp[1][i] = Math.max(dp[0][i-1], dp[0][i-2]) + sticker[1][i];
}
int max = Math.max(dp[0][N], dp[1][N]);
sb.append(max).append("\n");
}
System.out.print(sb);
}
}제가 짠 코드는 다음과 같습니다.
이 문제를 보고 저는 처음 백트래킹을 이용하여 풀면 되겠다는 생각을 하였습니다. 하지만 백트래킹을 이용하여 문제를 푼 결과 예제는 무리 없이 통과하였지만 시간 초과로 인해 문제를 푸는 것에 실패하였습니다.
이 문제의 분류를 확인한 순간 다이나믹 프로그래밍의 분류에 들어가 있는 것을 확인할 수 있었습니다.
그래서 dp라는 2차원 배열을 선언하여 이전에 있던 값 중에서 더했을 때 최고의 효율이 나오는 스티커들을 모아서 더하는 방법을 이용하여 이 문제를 해결하였습니다.
'알고리즘 > 다이나믹 프로그래밍' 카테고리의 다른 글
| 백준 9251번 : LCS java (0) | 2022.06.02 |
|---|---|
| 백준 12865번 : 평범한 배낭 java (0) | 2022.06.01 |
| 백준 1149번 : RGB거리 java (0) | 2022.05.27 |
| 백준 1932번 : 정수 삼각형 java (0) | 2022.05.27 |
| 백준 11660번 : 구간 합 구하기 5 java (0) | 2022.05.25 |




댓글