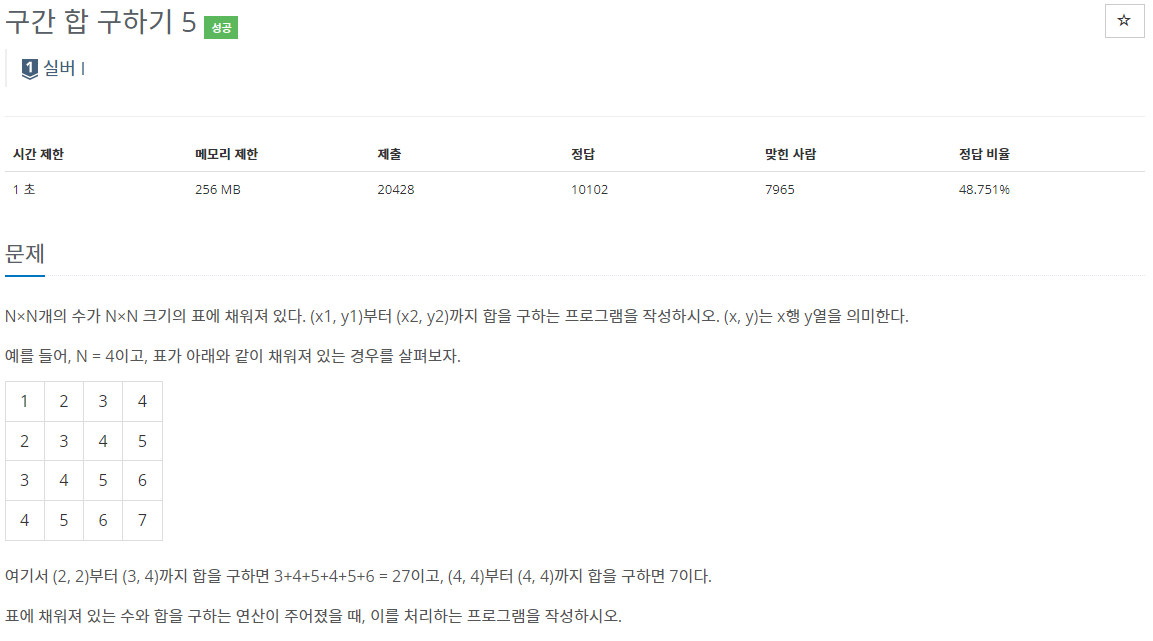
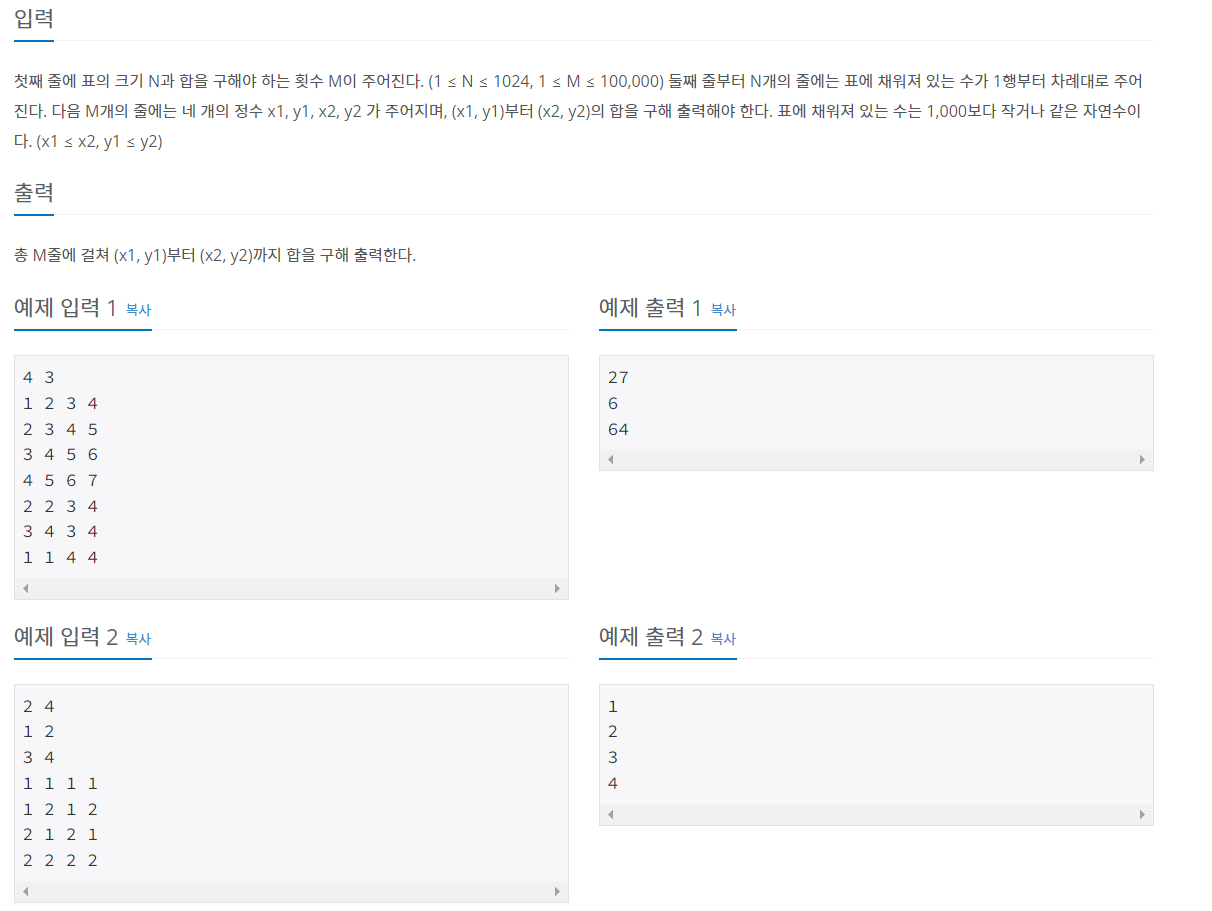
이 문제는 일정 범위의 구간 합을 미리 구해놓아서 원하는 범위의 합을 알고 싶을 때 빠르게 결과를 구하는 문제입니다.
저는 이 문제를 좌에서 우로 위에서 아래로 갈수록 수들을 합하여 저장해 놓도록 설계하였습니다.
아래에서 그림을 통해 자세히 설명드리도록 하겠습니다.
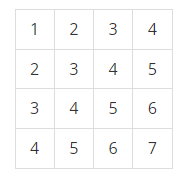
문제에 나와있는 예제로 구간 합을 구해보겠습니다.

위에서 설명드린 대로 화살표 방향으로 갈수록 값이 커집니다.
우선 가장 윗줄과 왼쪽 줄에서 구간합을 구하겠습니다.
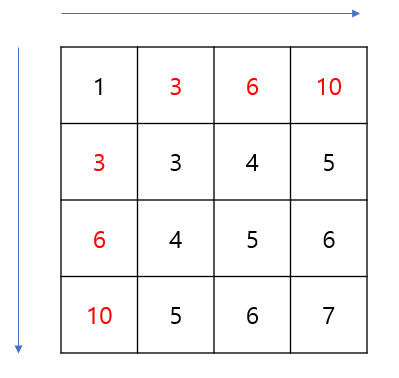
첫 번째 구간합에서는 윗 줄은 자신 왼쪽에 있던 수만 더하면 되고
왼쪽 줄은 자신의 위에 있던 수만 더하면 됩니다.
하지만 이 수들을 제외하고는 자신을 오른쪽 아래 꼭짓점으로 하는
사각형 안의 구간합을 구해야 합니다.

예를 들어 파란 박스 안에 있는 숫자가 있는 공간에는 빨간 박스 안에 있는 모든 수들의 구간합이 들어있어야 합니다.
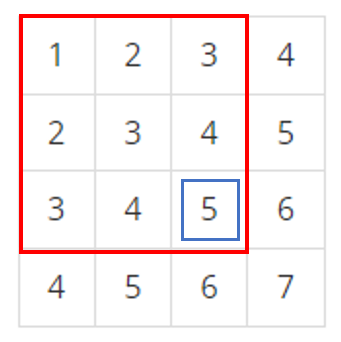
위의 그림에서는 구간합을 쉽게 구할 수 있지만 왼쪽 그림과 같은 영역의 구간합을 구하기 위해서는 어떻게 해야 할까요?
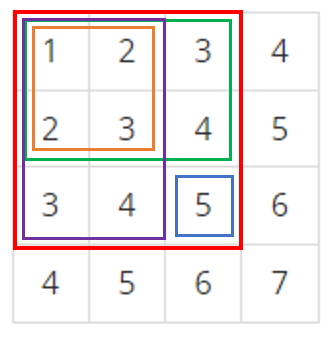
저는 이 빨간 박스 안의 구간합을 구하기 위해서 다음과 같이 각
구간들을 나누었습니다.
우선 숫자 5 위에 초록 박스의 구간합을 변수 sum에 더하고
숫자 5 왼쪽에 있는 보라색 박스를 변수 sum에 더한 후 파란색 박스의 값인 5를 sum에 더해주었습니다.
이렇게 하면 주황색 박스 안의 구간합들이 2번 더해지므로 sum에서 주황색 박스 안의 구간합을 빼주며 빨간 박스의 구간합을 구했습니다.

이런 식으로 표는 제가 원하는 구간합들을 채워 넣었습니다.
이제 문제에서 원하는 것처럼 (x1, y1)부터 (x2, y2)까지의 구간합을 구해야 합니다.
이 문제에서는 (x, y)는 x행 y열을 의미하지지만 저는 편의상 (x, y)를 y행 x열로 해석하였습니다.
(아래에서 나오는 괄호 안의 좌표는 이 문제에서는 (y, x)입니다.)
이제 (2, 2) 부터 (4, 4)까지의 구간합을 구해보겠습니다.
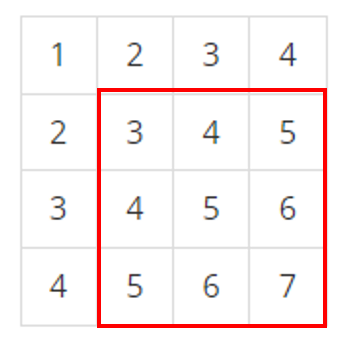
우리가 구해야하는 값은 빨간 박스 안의 구간합입니다.

우리는 이를 위해서 다음과 같이 구간을 나눕니다.
우선 보라색 박스의 구간합을 sumArray에서 가져옵니다.
여기서 주황색 박스 안의 구간합과 초록색 박스 안의 구간합을 보라색 박스의 구간합에서 빼줍니다.
마지막으로 2번 빠져 있는 파란색 박스의 구간합을 더해주면 됩니다.
이제 코드를 보여드리겠습니다.
import java.util.*;
import java.io.*;
public class Main{
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringBuffer sb = new StringBuffer();
String[] input = br.readLine().split(" ");
int N = Integer.parseInt(input[0]);
int num = Integer.parseInt(input[1]);
int[][] intArr = new int[N][N];
int[][] sumArr = new int[N][N];
for(int i = 0; i<N; i++){
StringTokenizer st = new StringTokenizer(br.readLine());
for(int j = 0; j<N; j++){
intArr[i][j] = Integer.parseInt(st.nextToken());
if(i == 0 && j == 0) {
sumArr[i][j] += intArr[i][j];
}
else if(i == 0)
sumArr[i][j] = sumArr[i][j-1] + intArr[i][j];
else if(j == 0)
sumArr[i][j] = sumArr[i-1][j] + intArr[i][j];
else
sumArr[i][j] = sumArr[i][j-1] + sumArr[i-1][j] - sumArr[i-1][j-1] + intArr[i][j];
}
}
for(int i = 0; i<num; i++){
StringTokenizer st = new StringTokenizer(br.readLine());
int y1 = Integer.parseInt(st.nextToken()) - 1;
int x1 = Integer.parseInt(st.nextToken()) - 1;
int y2 = Integer.parseInt(st.nextToken()) - 1;
int x2 = Integer.parseInt(st.nextToken()) - 1;
int sum = sumArr[y2][x2];
if(x1 == 0 && y1 == 0);
else if(x1 == 0)
sum -= sumArr[y1-1][x2];
else if(y1 == 0)
sum -= sumArr[y2][x1-1];
else{
sum -= sumArr[y2][x1-1] + sumArr[y1-1][x2];
sum += sumArr[y1-1][x1-1];
}
sb.append(sum).append("\n");
}
System.out.print(sb);
}
}저는 intArr에 입력받은 값을 넣었고 sumArr에 위에 설명드린 것과 같이 구간합을 넣었습니다. 그리고 y와 x의 순서를 반대로 입력받은 이유는 문제에서 주어진 값들을 내가 편하게 사용하기 위해서입니다.
문제를 풀면서 x1과 y1이 둘 다 0이 아니면 위에서 설명드린 방법대로 풀면 되지만 둘 중 하나라도 0이면 원하는 대로 결과가 나오지 않았었습니다.
따라서 이 두 경우를 따로 조건문으로 묶었습니다.
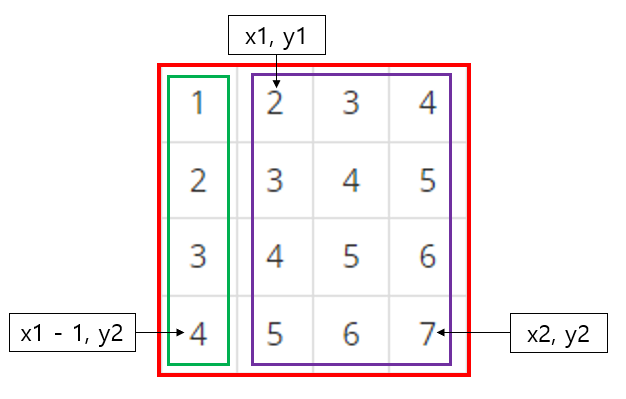
위의 그림과 같이 (1, 0) 부터 (4, 4)까지의 구간합은 빨간 박스의 구간합에서 초록 박스의 구간합을 빼는 식으로 문제를 해결하였습니다.
'알고리즘 > 다이나믹 프로그래밍' 카테고리의 다른 글
| 백준 9251번 : LCS java (0) | 2022.06.02 |
|---|---|
| 백준 12865번 : 평범한 배낭 java (0) | 2022.06.01 |
| 백준 1149번 : RGB거리 java (0) | 2022.05.27 |
| 백준 1932번 : 정수 삼각형 java (0) | 2022.05.27 |
| 백준 9465번 : 스티커 java (0) | 2022.05.26 |




댓글