

이 문제는 knapsack problem이라는 최적화 조합을 찾는 다이나믹 프로그래밍 문제입니다.
이 문제에서는 들 수 있는 무게가 정해져 있을 때 가장 가치합이 큰 값을 찾아내는 문제입니다.
저는 이 문제를 풀 때 특정한 무게에 따라서 각각의 물건들을 들 수 있는지를 따져가며 풀었습니다.
예제 1번을 통해서 그림과 같이 제가 이 문제를 푼 방식에 대해서 설명드리겠습니다.

예제 1번에서는 무게를 7kg까지 들 수 있고 물건이 4개가 주어진다고 하였기 때문에 다음과 같이 표를 그렸습니다.
무게가 0일 때는 아무것도 들 수 없고 물품이 0일 때는 아무 물건도 챙길 수 없다는 의미입니다.
따라서 무게가 0일 때와 물품이 0일 때의 셀에는 가치합이 0이 됩니다.

이제 각각의 무게에서 그 번호의 물품을 들 수 있는지를 확인해야 합니다.
예제의 입력에서 1번 물건의 무게와 가치는 (6, 13), 2번은 (4, 8), 3번은 (3, 6), 4번은 (5, 12)입니다.
이때 무게를 1, 2까지 들 수 있을 때 들 수 있는 물건은 없습니다.

이제 들 수 있는 무게가 3이 됐습니다. 물건을 1번까지 들 수 있을 때 1번 물건의 무게는 6이기 때문에 들 수 없습니다.
물건을 2번까지 들 때도 2번 물건의 무게도 4이기 때문에 들 수 없습니다.
물건을 이제 3번까지 들 수 있을 때 3번 물건의 무게는 3입니다. 따라서 준서는 이 물건을 들 수 있고 이 물건의 가치합은
6이니 무게가 3이고 물품이 3인 셀에 가치합 6을 넣어줍니다.
4번 물건까지 넣을 수 있을 때도 4번 물건의 무게가 5이기 때문에 들 수 없어서 가방에는 3번 물건만이 그대로
들어있습니다.
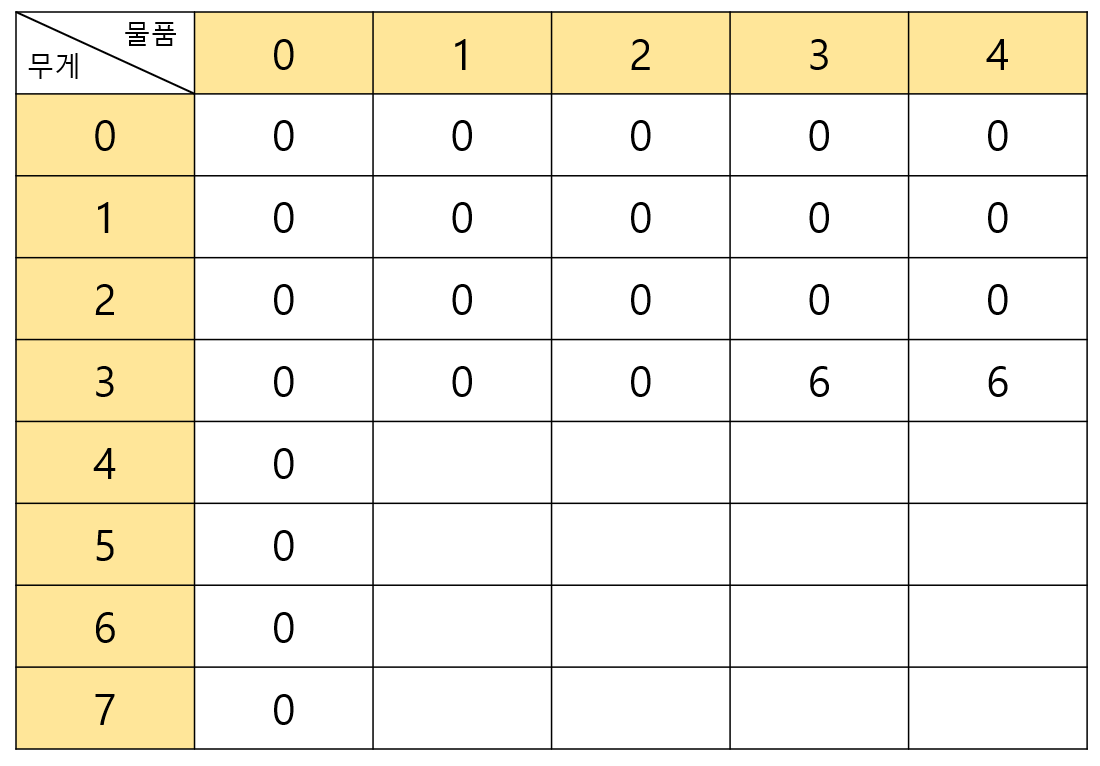
이제 무게가 4일 때는 살펴봅시다.
무게가 4일 때 1번 물건은 무게가 5이니 여전히 들 수 없습니다.
2번 물건을 들 때는 이제 물건의 무게가 4이니 들 수 있습니다. 이 물건의 가치는 8입니다.
3번 물건까지 들 수 있을 때부터 우리는 선택을 해야 합니다. 3번 물건의 무게는 3이고 가치는 6입니다. 2번 물건과
3번 물건 모두를 가방에 넣으면 좋겠지만 들 수 있는 무게는 4에 불과하니 가져갈 물건을 선택해야 합니다.
가방에 물건을 넣는 방법은 2가지가 있습니다. 무게가 3인 물건과 무게가 1인 물건 2개를 담는 것과 무게가 4인 물건
하나를 담는 것입니다.
이 2가지의 방법 중 가치합이 큰 것을 셀에 넣으면 됩니다. 하지만 이 문제에서는 무게가 1인 물건이 존재하지 않으므로
가치가 더 큰 2번 물건을 가져갑니다.
4번 물건까지 들 수 있을 때도 이와 같으므로 2번 물건만을 넣습니다.

무게를 5까지 들 수 있을 때도 이러한 방식으로 셀을 계속 채워줍니다.
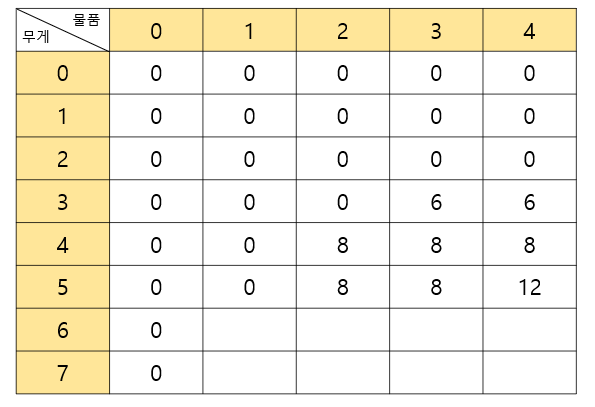
무게가 6일 때도 이와 같이 채웁니다.

무게가 7일 때는 이 과정을 조금 더 신경 써 주어야 합니다. 2번 물건과 3번 물건이 각각 무게가 4와 3 이므로 이 물건을
둘 다 가져가면 무게가 7이 되고 가치합이 14가 됩니다.

따라서 무게 7을 들 수 있을 때 가치합의 최댓값은 14가 됩니다.
이 과정을 코드로 표현하겠습니다.
import java.util.*;
import java.io.*;
public class Main{
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int N = Integer.parseInt(st.nextToken());
int K = Integer.parseInt(st.nextToken());
int[][] dp = new int[K+1][N+1];
int[] weight = new int[N+1];
int[] value = new int[N+1];
for(int i = 1; i<=N; i++){
st = new StringTokenizer(br.readLine());
weight[i] = Integer.parseInt(st.nextToken());
value[i] = Integer.parseInt(st.nextToken());
}
//i는 들 수 있는 무게, j는 물건의 idx
for(int i = 0; i<=K; i++){
for(int j = 0; j<=N; j++){
if(j == 0 || i == 0)
dp[i][j] = 0;
else if(weight[j]>i){
dp[i][j] = dp[i][j-1];
}
else{
dp[i][j] = Math.max(dp[i][j-1], value[j] + dp[i-weight[j]][j-1]);
}
}
}
System.out.println(dp[K][N]);
}
}이와 같이 위에 설명드린 내용들을 코드로 표현하였습니다.
if(j == 0 || i == 0)
dp[i][j] = 0;
else if(weight[j]>i){
dp[i][j] = dp[i][j-1];
}
else{
dp[i][j] = Math.max(dp[i][j-1], value[j] + dp[i-weight[j]][j-1]);
}그중에서 위의 내용에서 조금 유의하셔야 합니다.
if와 else if문은 이해를 쉽게 하실 겁니다.
else문은 dp[i][j-1] 즉 이전 물건 번호까지 넣었을 때의 값과 value[j] + dp[i-weight[j][j-1]을 비교해야 합니다.
value[j]는 그 번호의 물건을 넣었을 때의 가치입니다.
dp[i-weight[j][j-1]에서 i-weight[j]는 들 수 있는 무게인 i에서 j번 물건의 무게를 들었을 때의 무게를 빼준 값입니다.
dp[i-weight[j] 다음에 [j-1]을 해주는 이유는 j번 물건은 이미 value[j]를 더해주어 포함시켰기 때문에 이 물건을 제외하고
이전까지 물건들이 i-weight[j]의 무게일 때 가치합이 최대가 되는 것을 찾기 위해서입니다.
'알고리즘 > 다이나믹 프로그래밍' 카테고리의 다른 글
| 백준 1904번 : 01타일 java (0) | 2022.06.05 |
|---|---|
| 백준 9251번 : LCS java (0) | 2022.06.02 |
| 백준 1149번 : RGB거리 java (0) | 2022.05.27 |
| 백준 1932번 : 정수 삼각형 java (0) | 2022.05.27 |
| 백준 9465번 : 스티커 java (0) | 2022.05.26 |




댓글