

이 문제는 다익스트라 알고리즘을 이용하는 문제입니다.
다익스트라 알고리즘에 대하여 설명드리겠습니다.

예제 1번을 예시로 다익스트라 알고리즘을
설명드리겠습니다.
예제 1번에서는 왼쪽 그림과 같이 도시가
존재합니다.
이제 주어진 입력값에 맞게 버스를
배치하겠습니다.

입력값들을 전부 입력하면 다음과 같은
그림이 됩니다.
다익스트라 알고리즘은 '한 점'에서 다른
모든 점까지 각각의 거리의 최솟값을 정하는
알고리즘입니다.
이 말에 대해서 이 문제를 풀어보면 더 자세히 알려드리도록 하겠습니다.
예제 1번에서는 1번에서 시작하여 5번까지 갈 때의 버스 비용의 최솟값을 찾으라고 하였습니다.
따라서 우리는 다익스트라 알고리즘이 시작하는 점을 1번으로 둘 수 있습니다.
이제 1번에서 시작하는 버스들을 제외하고는 잠시 지우도록 하겠습니다.

1에서 출발하는 버스 노선을 제외하고는 모두 지운 그림입니다.
이미 거쳐가는 중간 지점으로 선택한 도시는 주황색 테두리로 바꾸었습니다.
표의 버스 비용은 1에서 각 도시로 갈 때 필요한 비용의 최소 비용입니다.
다익스트라 알고리즘은 한 점에서 출발할 때 이미 방문한 점을 제외한 인접한 도시 중에서 가는 데에 가장 적은 비용이
드는 도시를 선택한 후 이 도시를 중간 거점으로 삼아서 다른 도시로 갈 수 있는 최소 비용을 구합니다.
1이 시작 도시일 때 이미 방문하지 않았으며 갈 때의 비용이 가장 적은 도시는 4입니다.
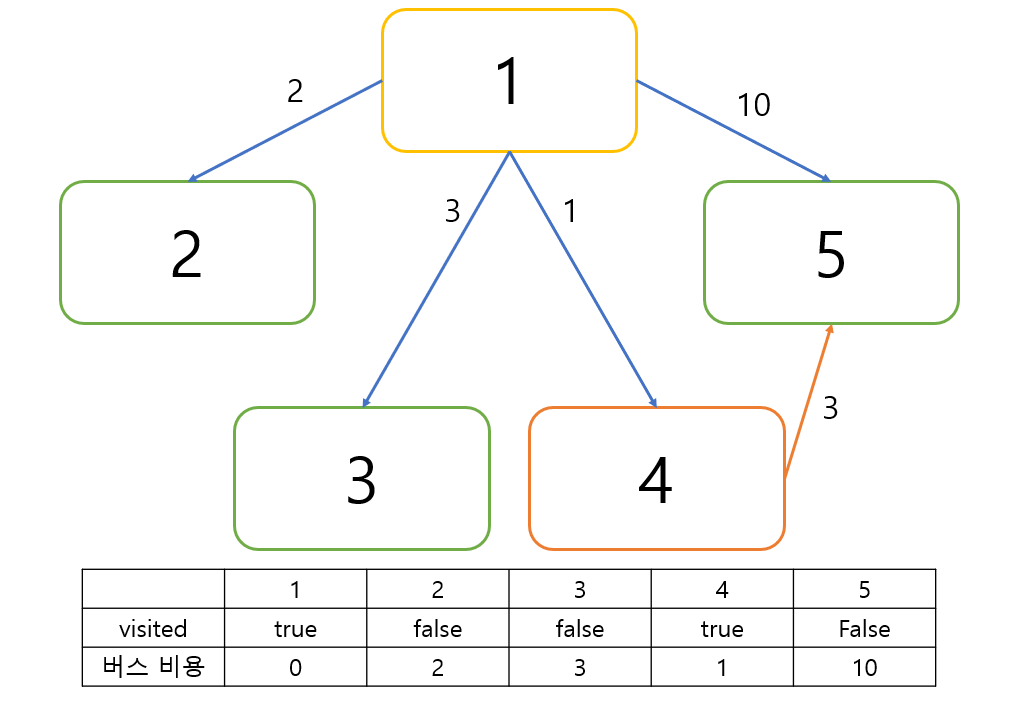
4를 거쳐서 다른 도시로 갈 때 4에서는 5로 갈 때 가중치가 3인 간선이 있습니다.
1에서 5로 바로 갈 때 버스 비용이 10인 반면 1에서 4를 거쳐 5로 갈 때는 1에서 4로 가는 비용 1에 4에서 5로 가는
비용인 3을 더하면 4밖에 안되므로 4를 거쳐 가는 것이 더 효율적입니다.
따라서 우리는 1에서 5로 바로 가는 간선을 포기하고 4를 거쳐가는 간선을 선택합니다.
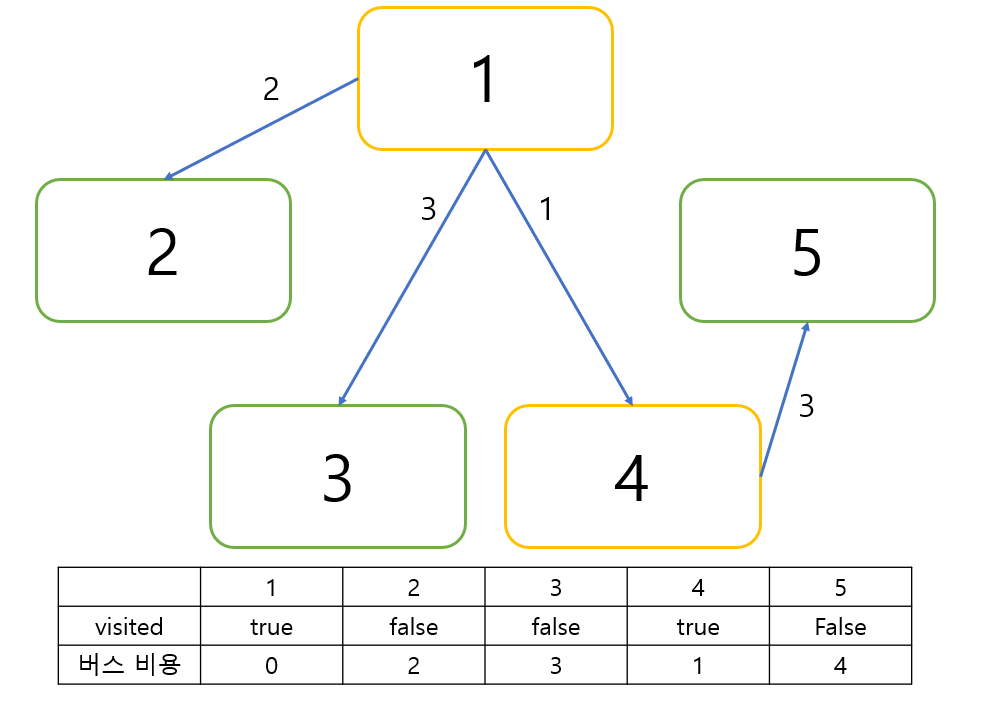
그럼 다음과 같은 그림이 됩니다.
이제 위에서 한 것과 같이 다음 도시를 선택해서 갈 수 있는 도시들을 확인하겠습니다.
1에서 이제 가지 않았고 버스 비용이 가장 적은 도시는 2입니다.

2를 중간 지점으로 선택할 때 2에서 4로 가는 버스 노선이 있지만 1에서 4로 바로 갈 때 버스 비용이 1인 데에 반해서
1에서 2를 거쳐 4로 갈 때 2 + 2 즉 4만큼의 비용이 드므로 이 노선은 사용하지 않습니다.
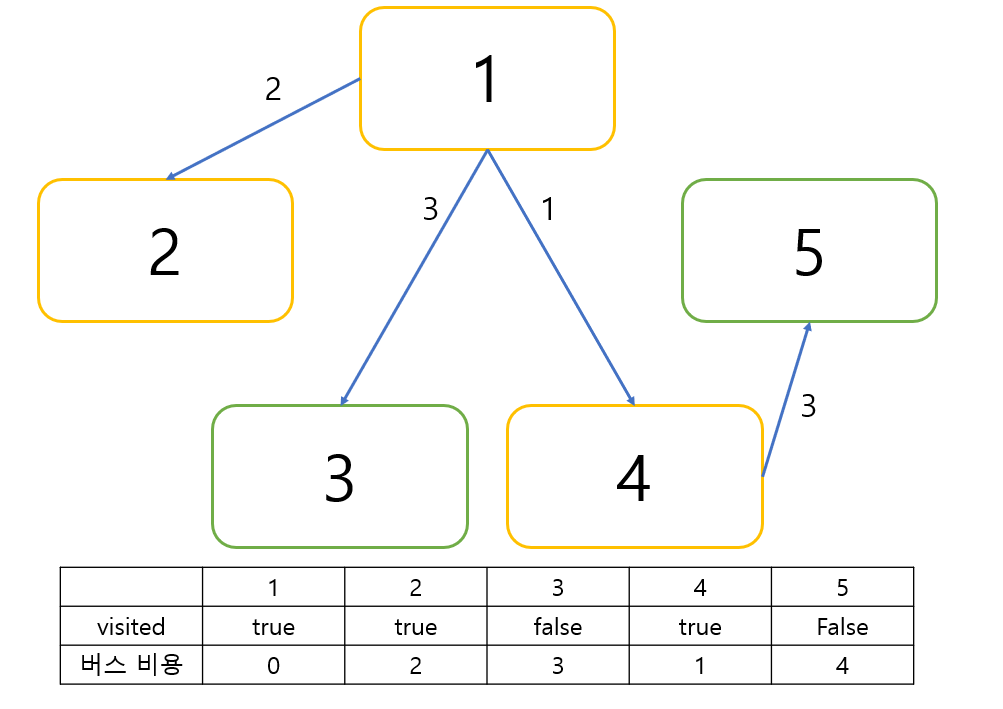
이제 다음 최소 버스 비용인 3번 도시를 선택하겠습니다.
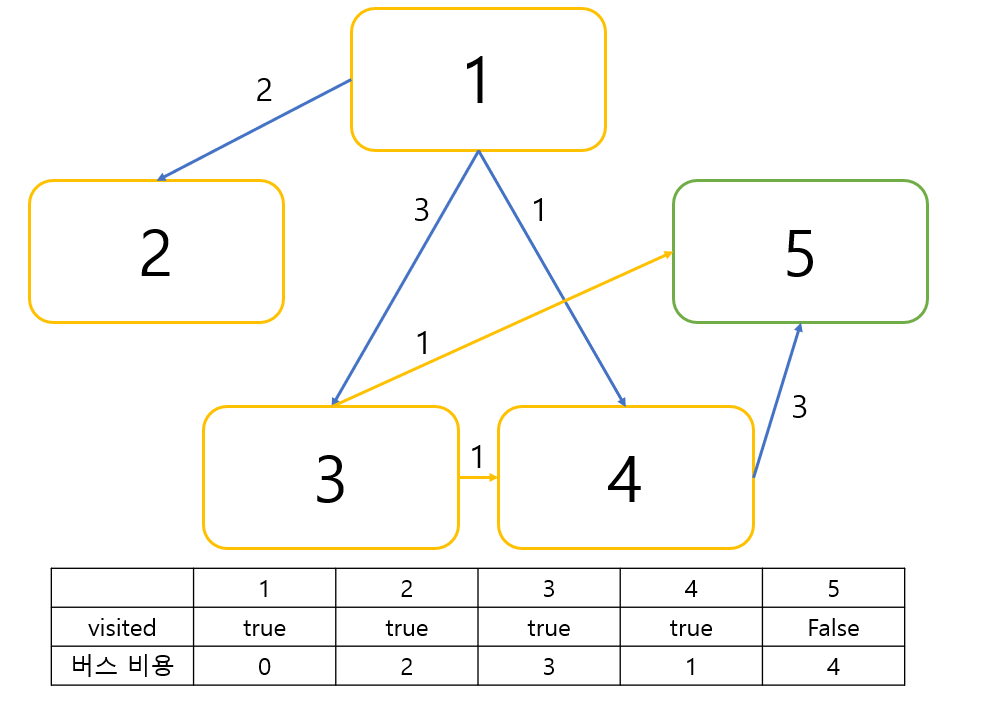
이번에도 주황색 노선들을 이용했을 때 원래보다 더 효율적인 동선은 없으므로 새로운 노선으로 바꾸지 않습니다.
이제 마지막 5번 도시를 중간 지점으로 삼겠습니다.
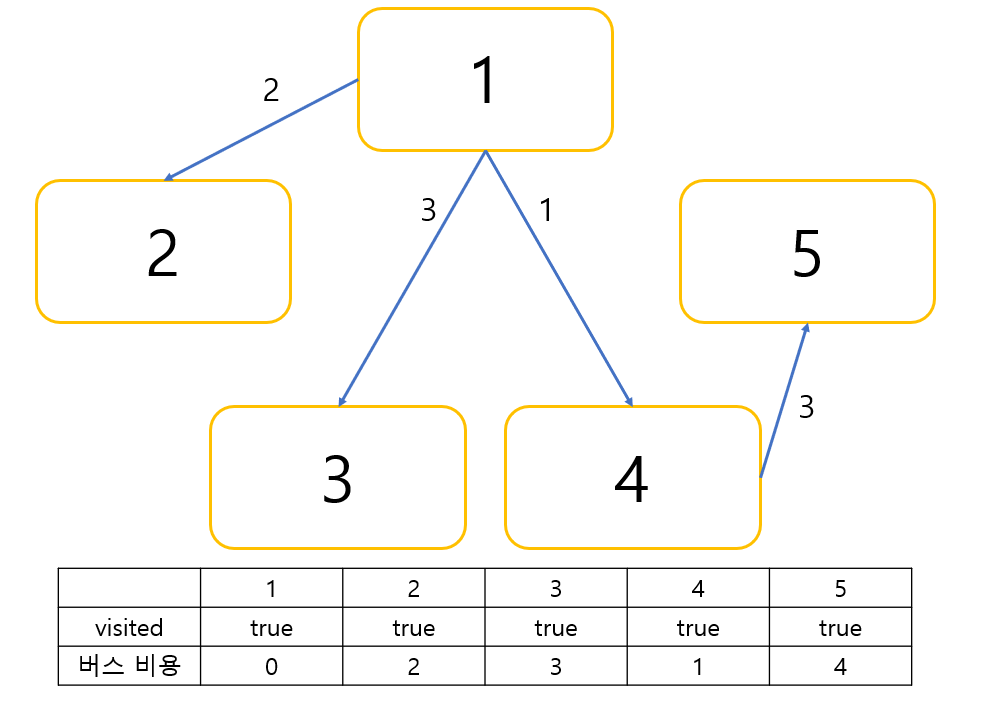
5번 도시에는 추가적인 버스 노선이 없습니다.
이제 다익스트라 알고리즘을 이용하여 1번 도시에서부터 각 도시까지의 최솟값들을 구했으므로 문제에서 원하는 1번
도시에서 5번 도시로의 버스 비용의 최솟값을 구하면 4입니다.
저는 이러한 알고리즘으로 이 문제를 해결하였습니다.
소스 코드를 보여드리겠습니다.
import java.util.*;
import java.io.*;
public class Main{
static int N;
static boolean[] visited;
static long[] dijkstra;
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
N = Integer.parseInt(br.readLine());
int M = Integer.parseInt(br.readLine());
long[][] map = new long[N][N];
for(int i = 0; i<N; i++)
for(int j = 0; j<N; j++){
if(i == j) {
map[i][j] = 0;
continue;
}
map[i][j] = Integer.MAX_VALUE;
}
for(int i = 0; i<M; i++){
StringTokenizer st = new StringTokenizer(br.readLine());
int row = Integer.parseInt(st.nextToken()) - 1;
int col = Integer.parseInt(st.nextToken()) - 1;
int val = Integer.parseInt(st.nextToken());
// 같은 경로가 여러 번 들어올 경우 가장 작은 weight 값을 저장
map[row][col] = Math.min(map[row][col], val);
}
StringTokenizer st = new StringTokenizer(br.readLine());
int start = Integer.parseInt(st.nextToken()) - 1;
int to = Integer.parseInt(st.nextToken()) - 1;
dijkstra = map[start].clone();
visited = new boolean[N];
visited[start] = true;
for(int i = 1; i<N; i++) {
int idx = choose();
visited[idx] = true;
for(int j = 0; j < N; j++)
if(!visited[j])
dijkstra[j] = Math.min(dijkstra[j], dijkstra[idx] + map[idx][j]);
}
System.out.println(dijkstra[to]);
}
static int choose(){
int minIdx = 0;
long min = Integer.MAX_VALUE;
for(int i = 0; i<N; i++){
if(visited[i])
continue;
if(min>dijkstra[i]){
min = dijkstra[i];
minIdx = i;
}
}
return minIdx;
}
}위에서 보여드린 다익스트라 알고리즘과 같이 문제를 풀었습니다.
이 문제를 풀 때 유의해야 할 점이 하나 있습니다.
for(int i = 0; i<N; i++)
for(int j = 0; j<N; j++){
if(i == j) {
map[i][j] = 0;
continue;
}
map[i][j] = Integer.MAX_VALUE;
}저는 이 위에 있는 map 배열을 초기화하는 부분에서 살짝 어려움을 겪었었습니다.
아무 버스 노선이 없는 공간에는 0이 들어가 있는데 저는 이를
map[i][j] = Integer.MAX_VALUE;다음과 같이 초기화해주었습니다.
처음 저는 map에 값을 넣을 때 입력받는 val 값이 99999가 최대라길래 그냥 적당히 큰 값을 넣으면 되지 않나 하는
마음으로 30만과 같은 값을 넣었었습니다.
당연히 문제는 틀렸었고 저는 잠시 생각해보고 그 이유를 알 수 있었습니다.
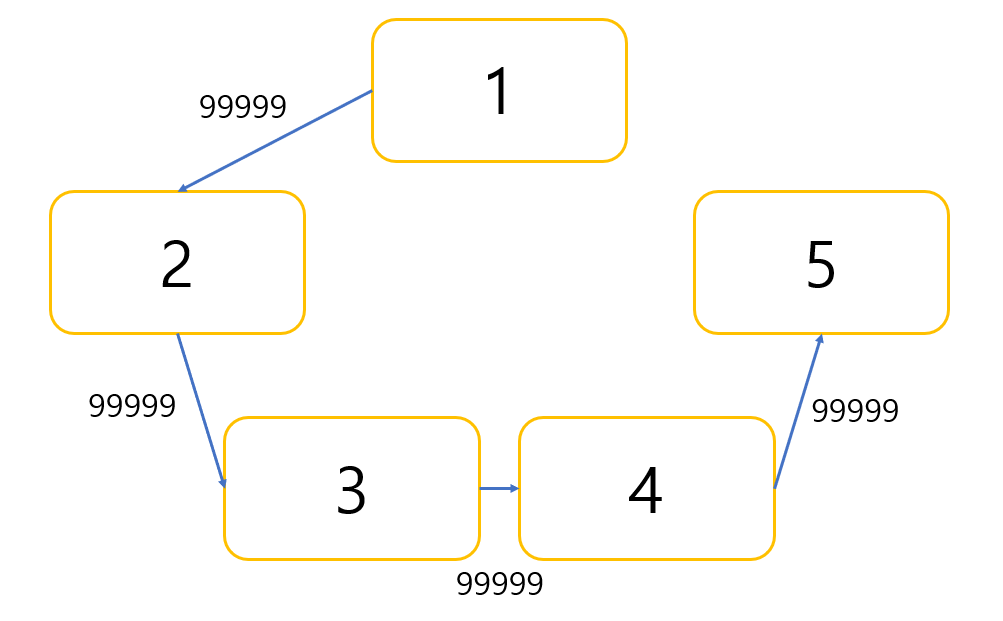
만약 최소 비용을 구하였을 때 다음과 같은 경우가 나온다면 처음 30만을 넣었을 때보다 훨씬 더 큰 버스 비용이 나올 수
있습니다.
따라서 99999 * (N-1)만큼의 버스 비용이 최대 버스 비용이므로 MAX_VALUE와 같은 안정적인 값을 넣어주어야 저와 같은 문제가 생기지 않으실 겁니다.
'알고리즘 > 다익스트라' 카테고리의 다른 글
| 백준 10282번 : 해킹 java (0) | 2022.07.15 |
|---|---|
| 백준 1504번 : 특정한 최단 경로 java (0) | 2022.06.25 |
| 백준 1238번 : 파티 java (0) | 2022.06.24 |
| 백준 14938번 : 서강그라운드 java (0) | 2022.06.11 |
| 백준 1753번 : 최단경로 java (0) | 2022.05.31 |




댓글