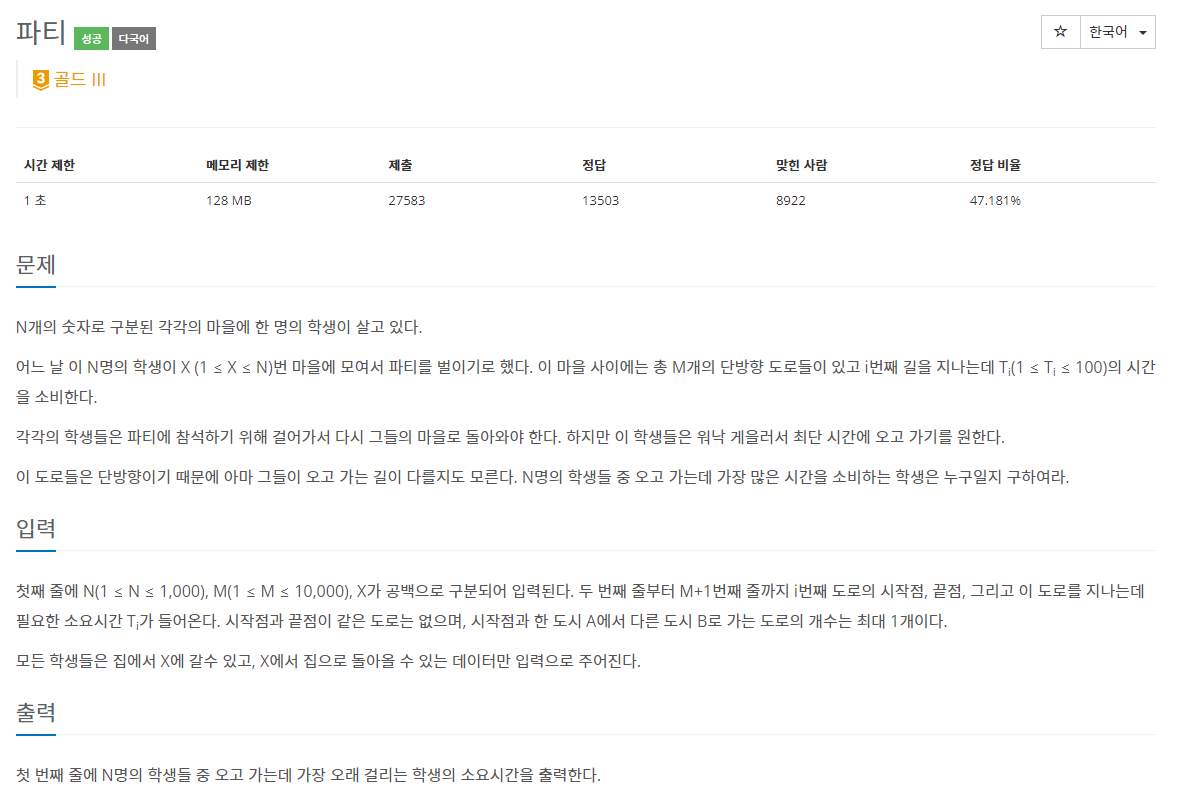
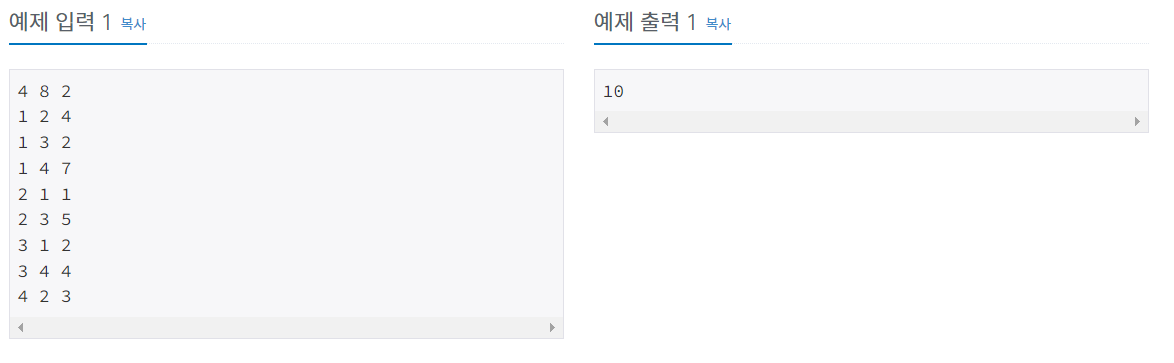
이 문제는 다익스트라 알고리즘을 이용하여 학생들이 파티를 참가하기 위해 한 마을로 모였다가 다시 자신의 마을로
돌아갈 때 가장 시간이 오래 걸리는 학생의 소요시간을 구하는 문제입니다.
이 문제를 푸는 방법은 2가지가 있습니다.
우선 첫 번째의 방법은 플로이드 와샬 알고리즘을 이용하여 각각의 학생들이 오고 갈 때의 시간을 구하는 방법이 있습니다.
하지만 이 방법을 사용한다면 시간 복잡도가 O(n^3)이 되어 시간이 오래 걸리게 됩니다.
이 문제에서는 플로이드 와샬 알고리즘을 써도 맞다고는 나오지만 N이 더 늘어나면 시간이 메모리를 더 많이 쓰게 되므로 좋은 정답이 아닙니다.
우선 플로이드 와샬 알고리즘으로 이 문제를 풀었을 때를 보여드리겠습니다.
import java.io.*;
import java.util.*;
public class Main {
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int N = Integer.parseInt(st.nextToken());
int M = Integer.parseInt(st.nextToken());
int X = Integer.parseInt(st.nextToken());
int[][] map = new int[N+1][N+1];
for(int i = 1; i<=N; i++){
for(int j = 1; j<=N; j++){
if(i == j)
map[i][j] = 0;
else
map[i][j] = Integer.MAX_VALUE;
}
}
for(int i = 0; i<M; i++){
st = new StringTokenizer(br.readLine());
int A = Integer.parseInt(st.nextToken());
int B = Integer.parseInt(st.nextToken());
int val = Integer.parseInt(st.nextToken());
map[A][B] = val;
}
for(int i = 1; i<=N; i++){
for(int j = 1; j<=N; j++){
for(int k = 1; k<=N; k++){
if(map[j][i] == Integer.MAX_VALUE)
continue;
if(map[i][k] == Integer.MAX_VALUE)
continue;
map[j][k] = Math.min(map[j][k], map[j][i] + map[i][k]);
}
}
}
int maxTime = Integer.MIN_VALUE;
for(int i = 1; i<=N; i++)
maxTime = Math.max(maxTime, map[i][X]+map[X][i]);
System.out.println(maxTime);
}
}
이 문제를 조금 더 효율적으로 풀기 위해서 다익스트라 알고리즘을 2번 사용합니다.
다익스트라 알고리즘은 한 점에서 다른 모든 점으로 갈 때의 거리의 최솟값을 구하게 해줍니다.
따라서 입력받은 값들로 X를 시작점으로 잡아 바로 다익스트라 알고리즘을 사용한다면 학생들이 자신의 마을로 돌아갈 때의 거리의 최솟값을 구할 수 있을 것입니다.
그리고 입력받을 때 입력받은 값들을 반대로 저장하는 리스트를 만듭니다.
예를 들어 2에서 3으로 가는데 5의 시간이 든다고 하면 3에서 2로 가는데 5의 시간이 든다고 표시합니다.
이 리스트를 이용하여 X를 시작점으로 하는 다익스트라 알고리즘을 실행하면 학생들이 자신의 마을에서 X로 올 때의 거리의 최솟값을 구할 수 있을 것입니다.
이를 이용한 코드를 보여드리겠습니다.
import java.io.*;
import java.util.*;
public class Main {
static int N, M;
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
int X = Integer.parseInt(st.nextToken());
List<List<Node>> list = new ArrayList<>();
List<List<Node>> reverseList = new ArrayList<>();
for(int i = 0; i<=N; i++){
list.add(new ArrayList<>());
reverseList.add(new ArrayList<>());
}
for(int i = 0; i<M; i++){
st = new StringTokenizer(br.readLine());
int A = Integer.parseInt(st.nextToken());
int B = Integer.parseInt(st.nextToken());
int val = Integer.parseInt(st.nextToken());
list.get(A).add(new Node(B, val));
reverseList.get(B).add(new Node(A, val));
}
int[] dist = dijkstra(list, X);
int[] reverseDist = dijkstra(reverseList, X);
int max = Integer.MIN_VALUE;
for(int i = 1; i <= N; i++)
max = Math.max(max, dist[i]+reverseDist[i]);
System.out.println(max);
}
static int[] dijkstra(List<List<Node>> l, int X){
int[] dist = new int[N+1];
Arrays.fill(dist, Integer.MAX_VALUE - 100);
dist[X] = 0;
boolean[] visited = new boolean[N+1];
Queue<Node> q = new PriorityQueue<>();
q.offer(new Node(X, 0));
while(!q.isEmpty()){
//a 노드가 중간에 거쳐갈 노드
Node a = q.poll();
if(visited[a.location])
continue;
visited[a.location] = true;
//nextNode가 노드 a를 거쳐 갈 노드
for(int i = 0; i<l.get(a.location).size(); i++){
Node nextNode = l.get(a.location).get(i);
if(dist[nextNode.location] > dist[a.location] + nextNode.val){
dist[nextNode.location] = dist[a.location] + nextNode.val;
q.offer(new Node(nextNode.location, dist[nextNode.location]));
}
}
}
return dist;
}
}
class Node implements Comparable<Node>{
int location, val;
Node(int location, int val){
this.location = location;
this.val = val;
}
@Override
public int compareTo(Node a){
return val - a.val;
}
}'알고리즘 > 다익스트라' 카테고리의 다른 글
| 백준 10282번 : 해킹 java (0) | 2022.07.15 |
|---|---|
| 백준 1504번 : 특정한 최단 경로 java (0) | 2022.06.25 |
| 백준 14938번 : 서강그라운드 java (0) | 2022.06.11 |
| 백준 1753번 : 최단경로 java (0) | 2022.05.31 |
| 백준 1916번 : 최소비용 구하기 java (0) | 2022.05.29 |




댓글