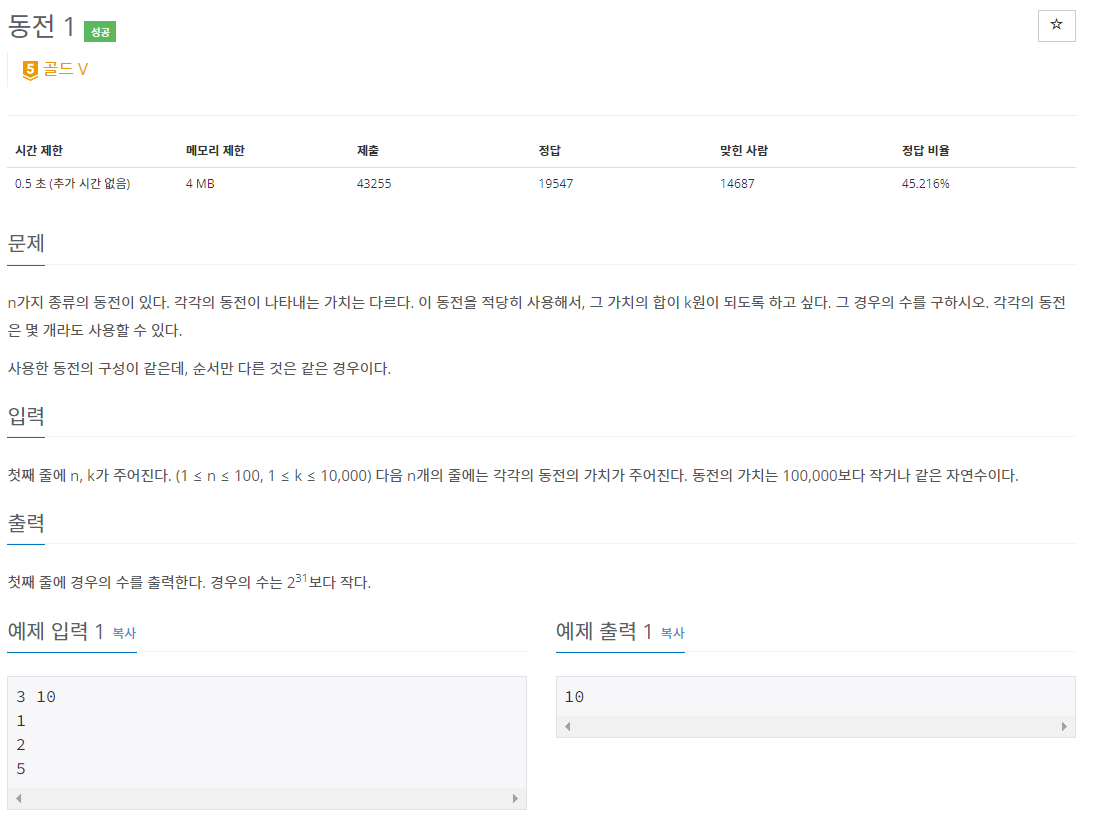
이 문제는 다이나믹 프로그래밍을 이용하여 N개의 동전을 이용하여 K원이 되게 하는 경우의 수를 구하는 문제입니다.
저는 이 문제를 N개의 동전의 가치들을 배열에 저장한 후 1원을 만들 때의 경우의 수부터 N원을 만들 때의 경우의 수를
각각의 동전을 사용할 수 있을 때로 나누어 구해주었습니다.
이에 대해서 예제 1번을 이용하여 자세히 설명드리겠습니다.
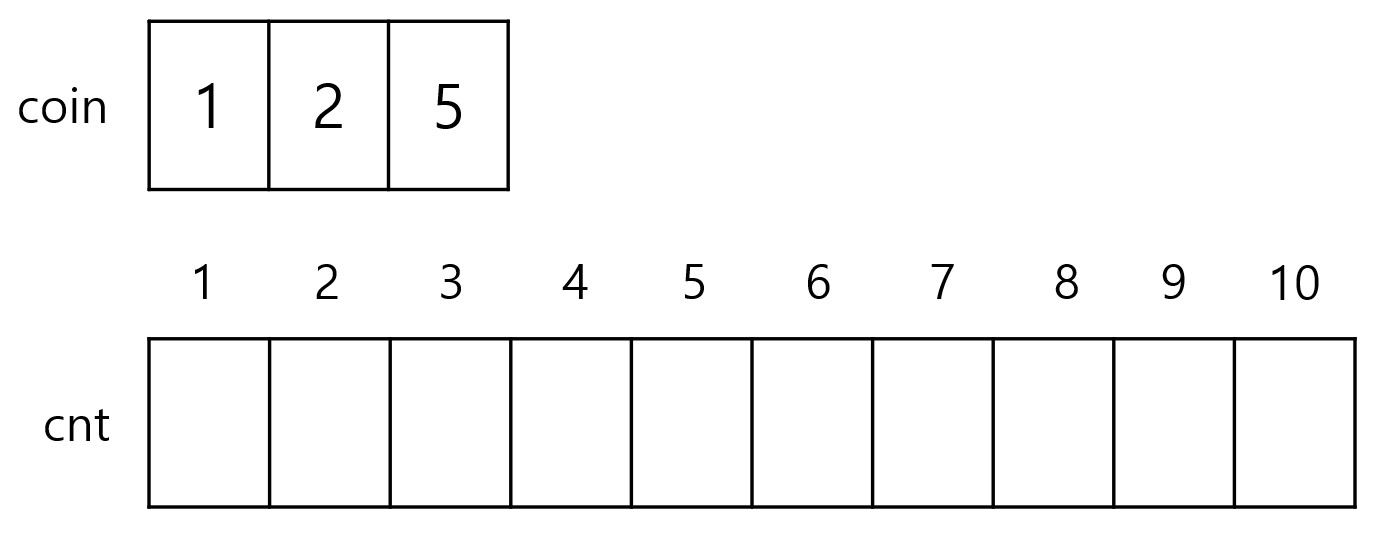
위의 예제 1번을 보시면 3개의 동전을 사용하여 가치의 합이 10이 될 때를 구해야 합니다.
우선 cnt 배열의 위에 있는 수는 각 셀에 들어갈 수 있는 가치의 최댓값을 나타낸 것입니다.
이제 코인의 가치 중 가장 가치가 낮은 1원짜리 동전으로만 cnt 배열을 채워보겠습니다.
cnt 배열을 채우는 점화식은 cnt[i] = cnt[i] + cnt[i-coin[j]]입니다.
이때 i는 가치의 합을 의미하고 j는 각각의 코인의 인덱스를 의미합니다.
위와 같은 점화식이 나오는 이유는 i가 7이고 j가 2여서 coin의 값이 2라고 했을 때 7을 만들기 위해서는 coin 2를 사용하지 않았을 때의 경우의 수에 5를 만든 다음 2를 추가한 경우의 수를 더해야 하기 때문입니다.
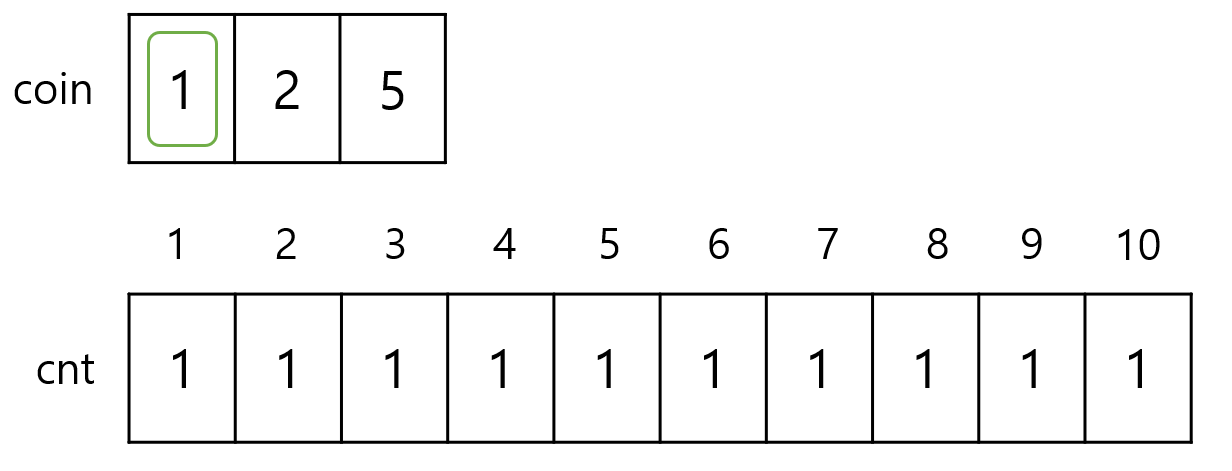
코인을 1 하나만 사용하였을 때는 모든 가치를 1로만 나타낼 수 있기 때문에 경우의 수는 모두 1입니다.
이제 2의 가치를 가진 코인도 이용하여 경우의 수를 나누어 보겠습니다.
2의 가치를 가진 코인을 사용할 때 가치 2를 나타내는 방법은 1+1과 2 가 있습니다.
3을 나타내는 법은 1+1+1과 1+2가 있습니다.
4를 나타내는 법은 1+1+1+1과 1+1+2, 2+2가 있습니다.
이런 방식으로 cnt를 채워보겠습니다.
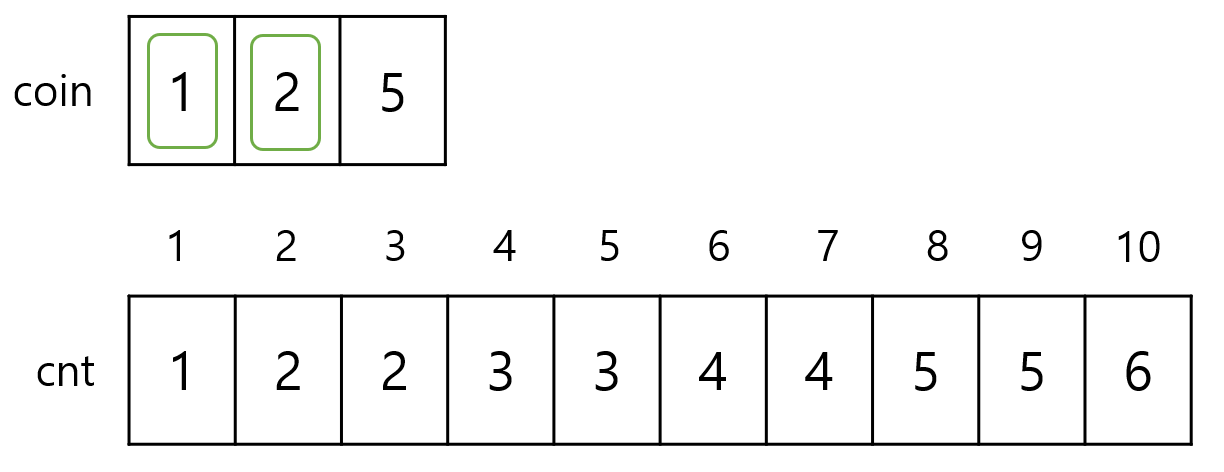
이제 마지막으로 5의 가치를 가진 동전을 사용할 때도 위에서 말씀드린 점화식인 cnt[i] = cnt[i] + cnt[i-coin[j]]을 이용해서
채워보도록 하겠습니다.
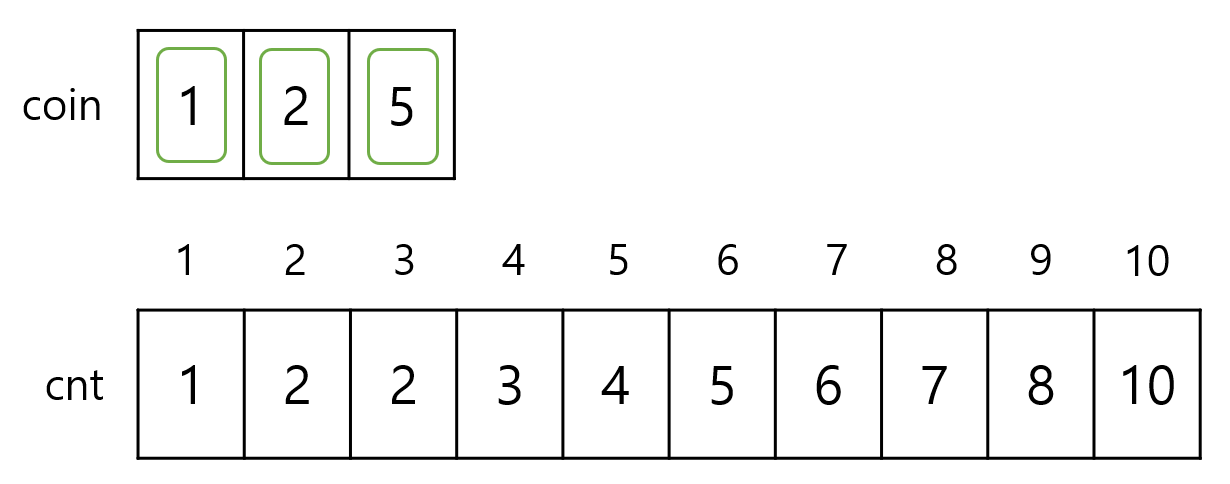
가치의 합이 10일 때를 구하면 cnt의 값은 10이 나옵니다.
이제 코드를 확인해보겠습니다.
import java.io.*;
import java.util.*;
public class Main {
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int N = Integer.parseInt(st.nextToken());
int K = Integer.parseInt(st.nextToken());
int[] coin = new int[N+1];
int[] cnt = new int[K+1];
cnt[0] = 1;
for(int i = 1; i<=N; i++)
coin[i] = Integer.parseInt(br.readLine());
//coin[] 을 전부 순회하면서 cnt를 더해줌
for(int i = 1; i<=N; i++){
//j는 현재 가질 수 있는 가치의 총량을 의미
for(int j = coin[0]; j<=K; j++){
if(j<coin[i])
continue;
cnt[j] += cnt[j-coin[i]];
}
}
System.out.println(cnt[K]);
}
}'알고리즘 > 다이나믹 프로그래밍' 카테고리의 다른 글
| 백준 2294번 동전 2 java (0) | 2022.06.15 |
|---|---|
| 백준 11052번 : 카드 구매하기 java (0) | 2022.06.14 |
| 백준 2096번 : 내려가기 java (0) | 2022.06.13 |
| 백준 11053번 : 가장 긴 증가하는 부분 수열 java (0) | 2022.06.08 |
| 백준 1912번 : 연속합 java (0) | 2022.06.07 |




댓글