반응형

이 문제는 깊이 우선 탐색을 이용해서 칸을 이동하면서 같은 알파벳이 적힌 칸을 두 번 지나지 않고 최대 갈 수 있는 칸을 구하는 문제입니다.
이 문제에 대해서 그림을 통해 자세히 설명드리도록 하겠습니다.

예제 1번을 표에 나타내면 위의 그림과 같습니다.
저는 이 문제를 풀 때 이미 지나간 알파벳은 set에 저장하여 다시 지나가지 않도록 했습니다.
ArrayList나 LinkedList는 contains 메소드에 대한 시간 복잡도가 O(n)입니다.
하지만 HashSet을 통해서 set을 구현하면 O(1)의 시간 복잡도로 contains 메소드를 사용 가능합니다.
따라서 set을 사용하지 않으면 시간 초과가 나므로 set을 사용하였습니다.
이 문제에서 시작점은 1행 1열이니 여기서 dfs를 시작합니다.
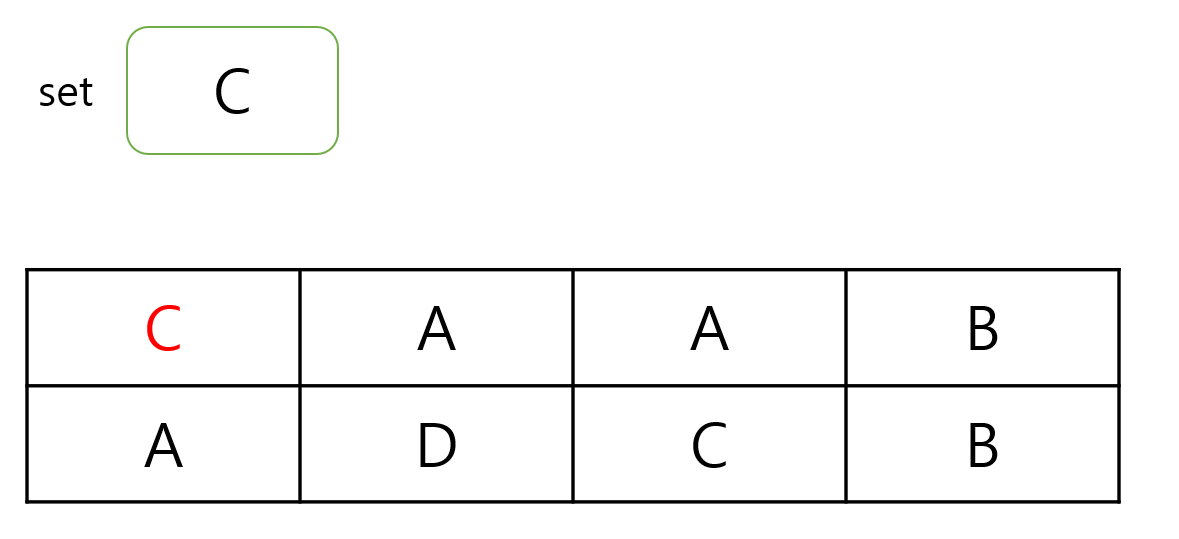
이제 주변을 탐색합니다.

A까지 탐색했을 때 1행 3열의 A는 탐색할 수 없기 때문에 D를 탐색합니다.

이제 주변에 탐색할 수 있는 칸이 없습니다.
따라서 이러한 입력이 주어졌을 때 갈 수 있는 칸의 최댓값은 3입니다.
이제 코드를 보여드리도록 하겠습니다.
import java.io.*;
import java.util.*;
public class Main {
static int R, C, max = 1;
static String[][] map;
static boolean[][] visited;
static Set<String> s = new HashSet<>();
static int[] dC = {1, -1, 0, 0};
static int[] dR = {0, 0, 1, -1};
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
R = Integer.parseInt(st.nextToken());
C = Integer.parseInt(st.nextToken());
map = new String[R][C];
visited = new boolean[R][C];
for(int i = 0; i<R; i++){
map[i] = br.readLine().split("");
}
s.add(map[0][0]);
visited[0][0] = true;
dfs(0, 0);
System.out.println(max);
}
static void dfs(int row, int col){
for(int i = 0; i<4; i++){
int dr = row + dR[i];
int dc = col + dC[i];
if(dr<0||dc<0||dr>=R||dc>=C)
continue;
if(visited[dr][dc])
continue;
if(s.contains(map[dr][dc]))
continue;
s.add(map[dr][dc]);
visited[dr][dc] = true;
max = Math.max(max, s.size());
dfs(dr, dc);
s.remove(map[dr][dc]);
visited[dr][dc] = false;
}
}
}소요되는 시간을 줄이기 위해서 set을 사용한다는 것만 조심하면 어려운 것은 없는 문제였습니다.
반응형
'알고리즘 > 깊이 우선 탐색(dfs)' 카테고리의 다른 글
| 백준 2644번 : 촌수계산 java (0) | 2022.07.07 |
|---|---|
| 백준 1707번 : 이분 그래프 java (0) | 2022.06.30 |
| 백준 4963번 : 섬의 개수 java (0) | 2022.06.09 |
| 백준 1967번 : 트리의 지름 java (0) | 2022.06.08 |
| 백준 17070번 : 파이프 옮기기 1 java (0) | 2022.06.06 |




댓글