

이 문제는 각각의 번호마다 다익스트라 알고리즘을 적용하여 각각의 정점마다 다른 정점까지 갈 때의 최단경로에서 처음으로 거쳐가는 정점을 출력하는 문제입니다.
저는 최단 경로에서 처음 거쳐가는 정점을 구하기 위해서 firstGo라는 배열을 따로 만들어서 이 정점에 오기 위해서 처음 거쳐야 하는 정점을 저장하게 만들었습니다.
이 firstGo라는 배열은 초기값으로 자기 자신의 정점 번호를 가지고 있습니다.
그리고 시작 정점에서 다른 정점을 거쳐서 자신의 정점으로 오는 것이 더 효율적이라면 firstGo 배열에서 그 정점의 인덱스에 저장되어 있는 정점을 저장하게 하는 식으로 최단 경로에서 처음 간 정점을 구하게 만들었습니다.

위의 그림과 같은 그래프가 있다고 가정하겠습니다.
이 그래프를 이용하여 다익스트라 알고리즘을 실행할 때 처음 정점은 1입니다.

따라서 1번 정점에서 바로 다른 정점을 갈 때의 거리를 dist 배열에 담으면 다음과 같습니다.
이제 다익스트라 알고리즘을 이용해야 하기 때문에 방문하지 않은 정점 중에서 시작 정점에서 가장 거리가 작은 정점인 2번 정점을 포함하여 다른 정점으로의 거리를 확인하겠습니다.
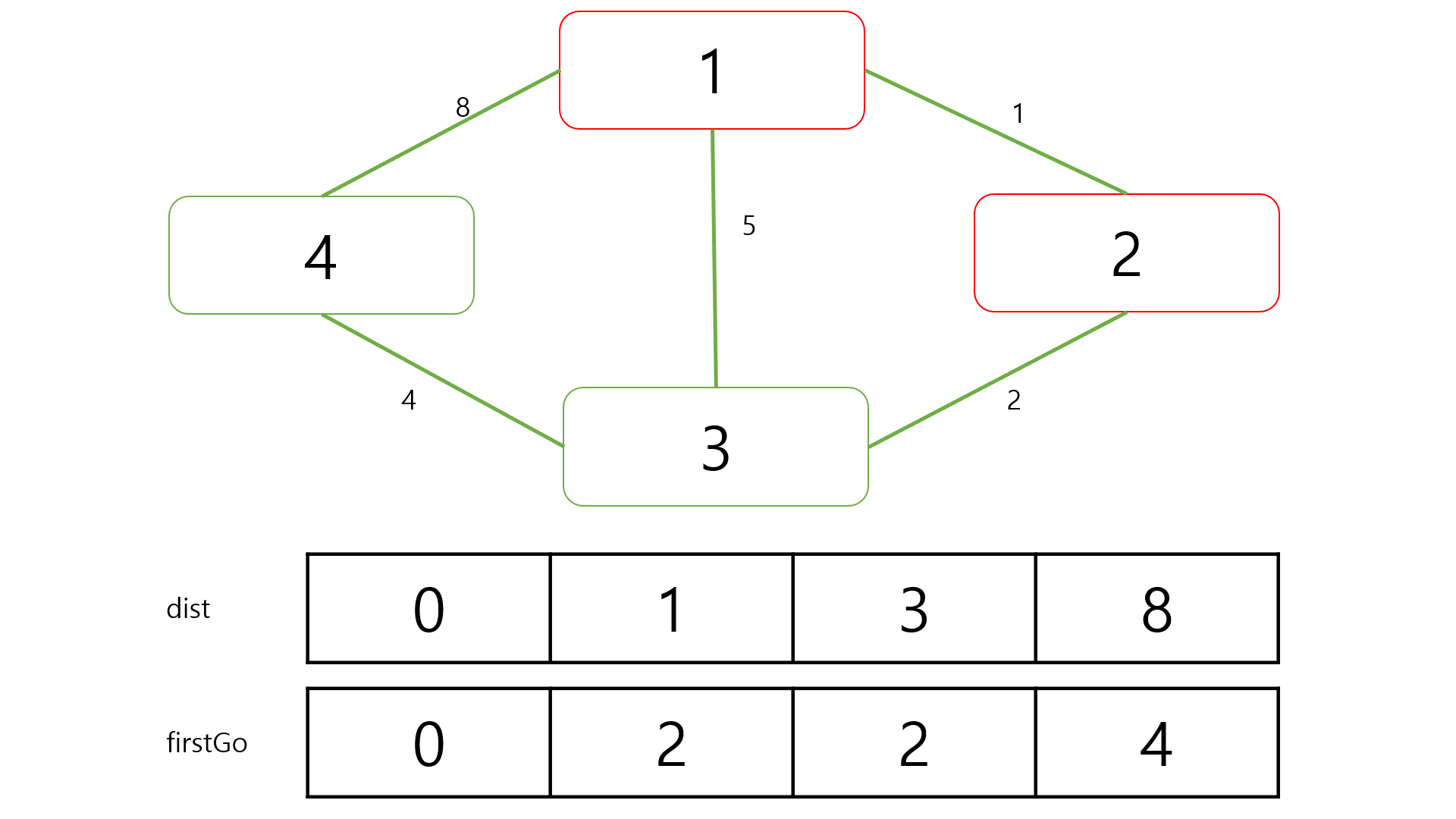
1번 정점에서 3번 정점으로 바로 가는 것보다 2번 정점을 거쳐서 가는 것이 더 거리가 짧으므로 dist 배열을 바꿔줍니다.
또한 2번 정점을 통해서 가는 것이 효율적이므로 firstGo에서 3번 정점의 값을 fistGo에서 2번 정점이 가지고 있는 값으로 바꾸어줍니다.
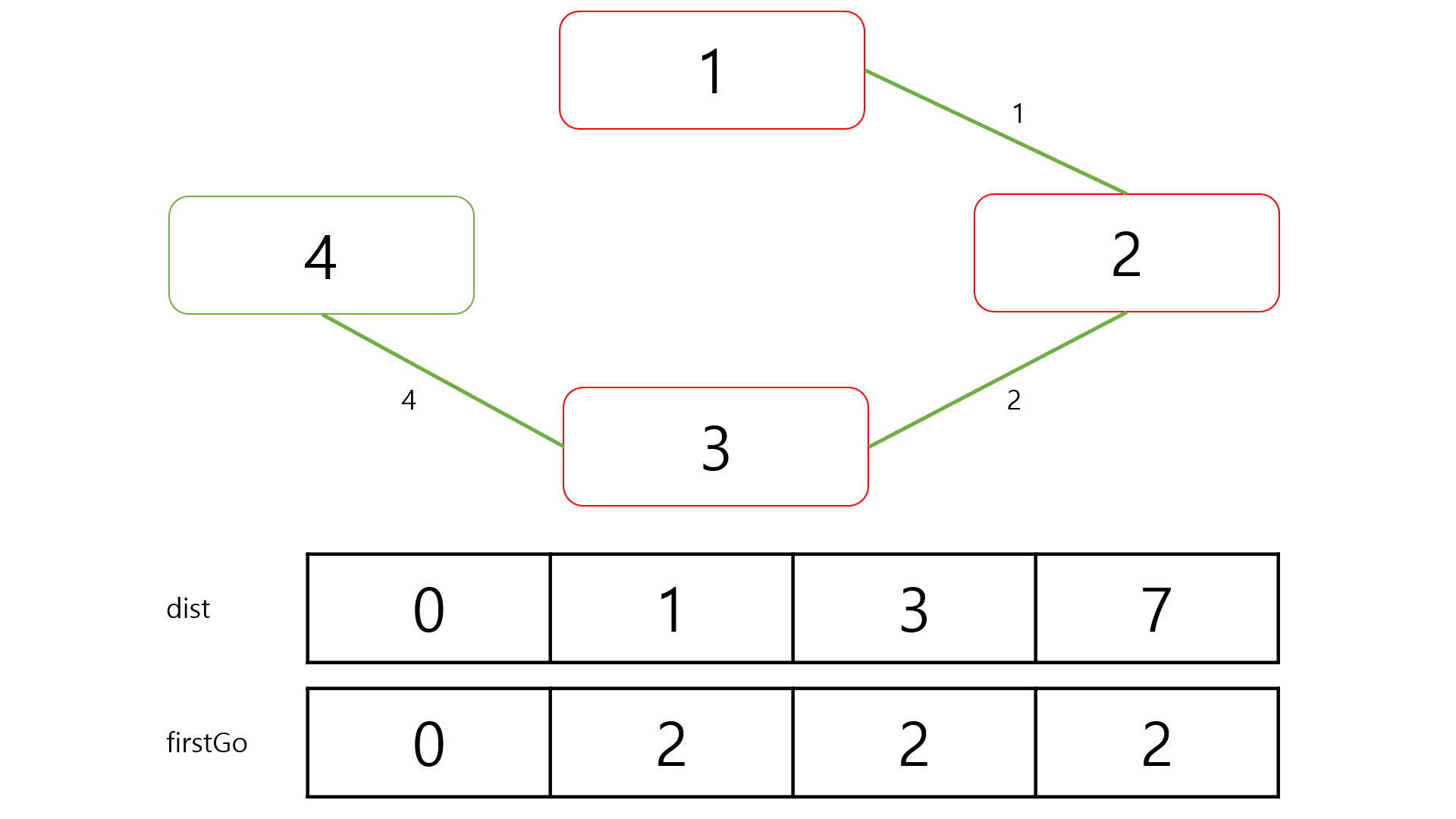
그다음 3번 정점을 거쳐서 다른 정점으로 가는 경로를 찾아볼 때 4번 정점으로 갈 때 원래의 경로보다 3번 정점을 거쳐서 가는 것이 더 효율적입니다.
따라서 dist에서 4번 정점의 값을 초기화해주고 firstGo 배열에서 3번 정점이 가지고 있는 값으로 4번 정점의 firstGo 값을 바꾸어줍니다.
4번 정점을 통해서 추가로 갈 수 있는 곳이 없으므로 1번 정점을 시작 정점으로 하는 다익스트라 알고리즘을 종료합니다.
이러한 과정을 시작 정점을 다른 정점으로 계속 바꾸어 주면서 실행해주면 이 문제를 해결하실 수 있습니다.
import java.io.*;
import java.util.*;
public class Main {
static int N;
static List<List<Node>> l = new ArrayList<>();
static int[] firstGo;
static int[] dist;
static int[][] answer;
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
int M = Integer.parseInt(st.nextToken());
for(int i = 0; i<=N; i++)
l.add(new ArrayList<>());
answer = new int[N+1][N+1];
while(M-->0){
st = new StringTokenizer(br.readLine());
int A = Integer.parseInt(st.nextToken());
int B = Integer.parseInt(st.nextToken());
int val = Integer.parseInt(st.nextToken());
l.get(A).add(new Node(B, val));
l.get(B).add(new Node(A, val));
}
for(int i = 1; i<=N; i++)
dijkstra(i);
for(int i = 1; i<=N; i++){
for(int j = 1; j<=N; j++) {
if(i == j)
System.out.print("- ");
else
System.out.print(answer[i][j] + " ");
}
System.out.println();
}
}
static void dijkstra(int vertex){
firstGo = new int[N+1];
for(int i = 1; i<=N; i++) {
if(i == vertex)
firstGo[i] = 0;
else
firstGo[i] = i;
}
dist = new int[N+1];
for(int i = 1; i<=N; i++){
if(i == vertex)
dist[i] = 0;
else
dist[i] = Integer.MAX_VALUE;
}
Queue<Node> q = new PriorityQueue<>();
q.offer(new Node(vertex, 0));
while(!q.isEmpty()){
Node a = q.poll();
for(int i = 0; i<l.get(a.vertex).size(); i++){
Node nextV = l.get(a.vertex).get(i);
if(dist[nextV.vertex] > dist[a.vertex] + nextV.value){
dist[nextV.vertex] = dist[a.vertex] + nextV.value;
q.offer(new Node(nextV.vertex, dist[nextV.vertex]));
//처음 while문을 반복할 때를 제거
if(a.vertex == vertex)
continue;
firstGo[nextV.vertex] = firstGo[a.vertex];
}
}
}
for(int i = 1; i<=N; i++)
answer[vertex][i] = firstGo[i];
}
}
class Node implements Comparable<Node>{
int vertex, value;
Node(int vertex, int value){
this.vertex = vertex;
this.value = value;
}
@Override
public int compareTo(Node a){
return this.value - a.value;
}
}'알고리즘 > 다익스트라' 카테고리의 다른 글
| 백준 2211번 : 네트워크 복구 java (0) | 2022.07.27 |
|---|---|
| 백준 5972번 : 택배 배송 java (0) | 2022.07.22 |
| 백준 4485번 : 녹색 옷 입은 애가 젤다지? java (0) | 2022.07.21 |
| 백준 10282번 : 해킹 java (0) | 2022.07.15 |
| 백준 1504번 : 특정한 최단 경로 java (0) | 2022.06.25 |




댓글