

이 문제는 유명한 하노이 탑을 움직이는 문제입니다. 하노이 탑을 옮기는 규칙을 옮기는 원판이 3개일 때로 예를 들어 설명하겠습니다.
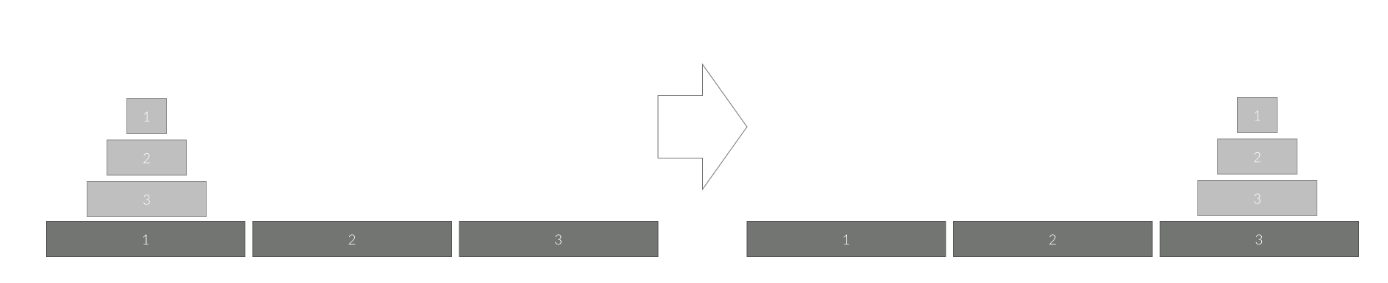
위의 그림과 같이 옮기고자 하는 과정을 그림으로 보여드리겠습니다.

우선 처음 상황입니다.
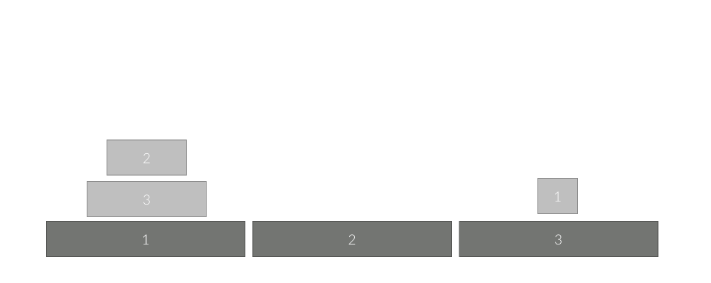
그다음 1번 원판을 1번 자리에서 3번 자리로 옮깁니다.
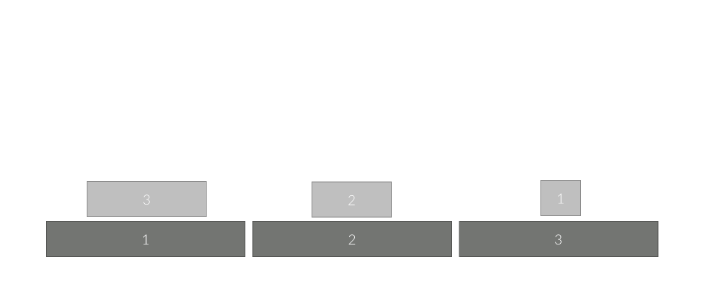
2번 원판을 1번 자리에서 2번 자리로 옮깁니다.

1번 원판을 3번 자리에서 2번 자리로 옮깁니다.
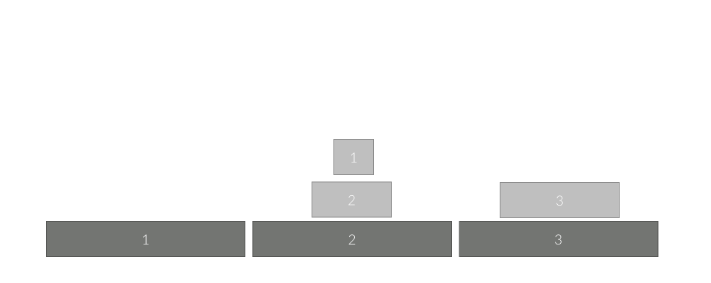
그 다음 3번 원판을 1번에서 3번 자리로 옮깁니다.
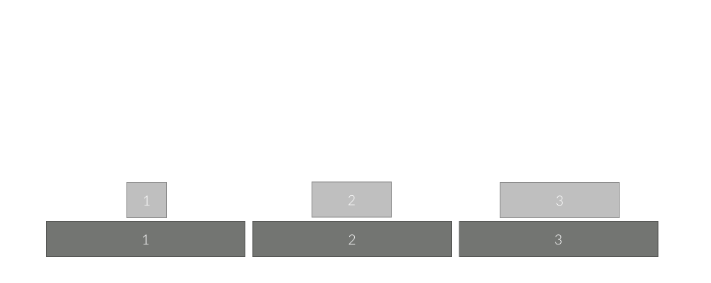
1번 원판을 2번 자리에서 1번 자리로 옮깁니다.
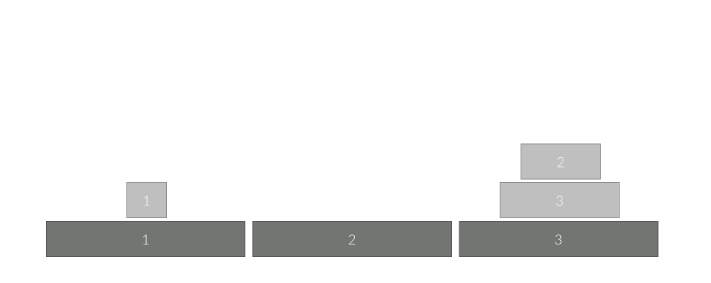
2번 원판을 2번 자리에서 3번 자리로 옮깁니다.
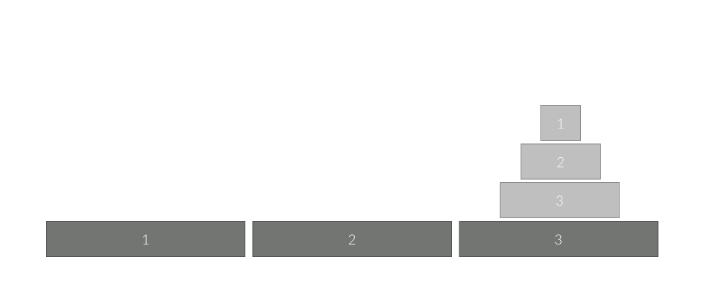
이제 1번 원판을 1번 자리에서 3번으로 옮기면 이동이 완료되었습니다.
예시와 같이 7번의 이동으로 3개의 원판이 이동되었습니다.
그런데 이렇게 3개의 원판을 옮기는 과정은 아래의 그림과 같이 가장 아래에 있는 원판 1개를 제외하고 나머지 원판을 중간 지점으로 보내 놓고 가장 아래의 원판을 목표 지점으로 옮긴 후 나머지를 목표 지점으로 옮기는 것으로 표현할 수 있습니다.

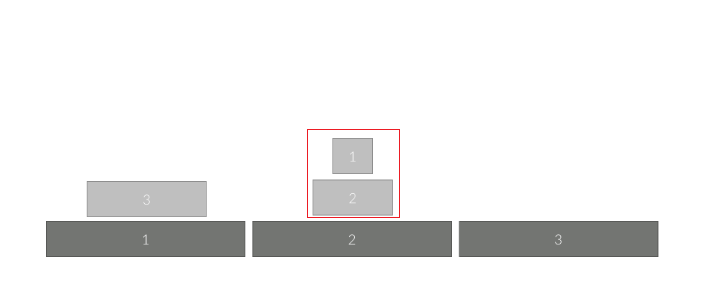
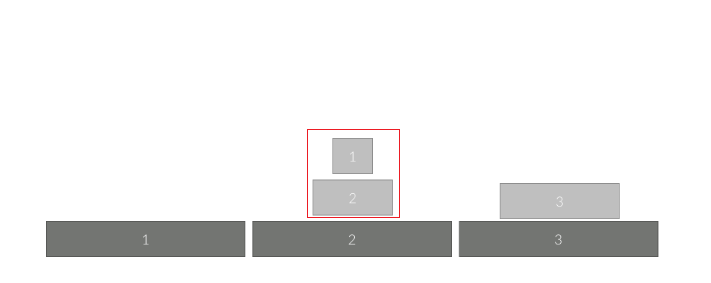
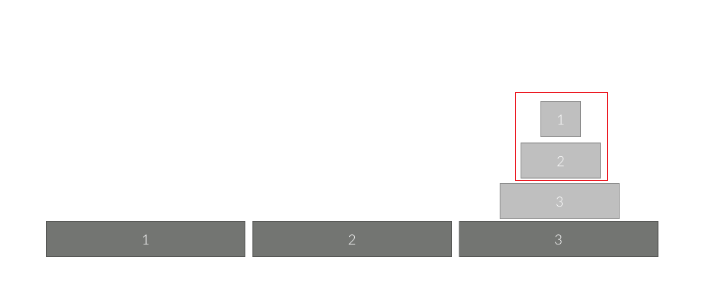
이 그림들은 위에 하노이 탑을 옮기는 과정 중간중간에 있는 그림들과 같습니다.
여기서 우리는 하노이 탑 문제가 높이가 N인 탑을 옮기려면 N-1의 높이를 가진 탑을 중간으로 옮긴 후 아래의 한 칸을 목표로 보낸 후 다시 N-1의 높이를 가진 탑이 목표지점으로 가면 해결할 수 있다는 것을 알 수 있습니다.
이를 아래와 같이 코드로 만들 수 있습니다.
import java.io.*;
public class Main{
static StringBuffer sb;
static int cnt = 0;
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
sb = new StringBuffer();
int N = Integer.parseInt(br.readLine());
hanoi(1, 2, 3, N);
System.out.println(cnt);
System.out.print(sb);
}
static void hanoi(int from, int use, int to, int N){
if(N == 1) {
cnt++;
sb.append(from+" "+to).append("\n");
return;
}
hanoi(from, to, use, N-1);
sb.append(from+" "+to).append("\n");
cnt++;
hanoi(use, from, to, N-1);
}
}재귀를 이용하여 N-1 높이의 탑을 옮기고 가장 아래의 칸을 옮긴 후 다시 N-1 높이의 탑을 옮기는 것을 표현했습니다.
여기서 이동 경로를 출력할 때마다 cnt값을 늘려준 이유는 몇 번 이동이 실행되었는지 확인하기 위해서입니다.
'알고리즘 > 구현' 카테고리의 다른 글
| 백준 13335번 : 트럭 java (0) | 2022.06.16 |
|---|---|
| 백준 14503번 : 로봇 청소기 java (0) | 2022.06.16 |
| 백준 17144번 : 미세먼지 안녕! java (0) | 2022.06.09 |
| 백준 1138번 : 한 줄로 서기 java (0) | 2022.06.07 |
| 백준 14500번 : 테트로미노 java (0) | 2022.05.25 |




댓글